Elmo
- 37
- 6
- TL;DR Summary
- Need help in understanding the operator product expansion as shown in Schwartz
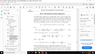
I have included here the screen shot of the page I am referring to.I am unsure of how this non-local Lagrangian of Eqtn(32.68) has been constructed. Have they just integrated the interaction Lagrangian densities over two different sets of points (x & y) ?
If so, then why is there no P_L in there, why just a gamma matrix ?
And in this Eqtn(32.68) have they used the full electroweak theory ?
The paragraph above claims that they have integrated out the W boson ,then got this expression but then why have the written the W propagator in there as well ?
In the next step Eqtn(32.69) I don't get how the expression for the propagator is modified ie where does the DeAlembertian come from ?
From this it seems to me that the thing responsible for converting a non-local Lagrangian to a local one,is simply the position space delta function resulting from the momentum integral of the exponential.
From what I understand, the interaction due to the full electroweak Lagrangian should be non-local while for the lower energy 4 Fermi theory, it should be local. So would the answer have been the same had they used the 4 Fermi theory instead ?
If so, then why is there no P_L in there, why just a gamma matrix ?
And in this Eqtn(32.68) have they used the full electroweak theory ?
The paragraph above claims that they have integrated out the W boson ,then got this expression but then why have the written the W propagator in there as well ?
In the next step Eqtn(32.69) I don't get how the expression for the propagator is modified ie where does the DeAlembertian come from ?
From this it seems to me that the thing responsible for converting a non-local Lagrangian to a local one,is simply the position space delta function resulting from the momentum integral of the exponential.
From what I understand, the interaction due to the full electroweak Lagrangian should be non-local while for the lower energy 4 Fermi theory, it should be local. So would the answer have been the same had they used the 4 Fermi theory instead ?