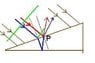
- #1
fluidistic
Gold Member
- 3,949
- 264
Homework Statement
See pictures for the data.
Basically there's a transparent prism looking like an inclined plane and making an angle [tex]\alpha[/tex] with the horizontal. Its base is 3 cm large and if we shine a vertical light of wavelength [tex]\lambda[/tex], we can observe an interference pattern as seen in the figure. If the interference pattern is 1 cm large, what is [tex]\alpha[/tex] worth?
Give the intensity of light in the interference pattern.
Figure out why do we only see an interference pattern in 1 cm despite shining light over the whole prism.
Homework Equations
No idea.
The Attempt at a Solution
I've absolutely no idea how to start this. In fact I don't understand where the interference pattern is (can we see it because of a diffusion somewhere in the prism?!). Is it at the base of the prism? Why is there interference?!
I know there's refraction of light through the inclined surface and then there's a reflection (Changing the phase of [tex]\pm \pi[/tex] rad or not? I know reflection causes a change in angle's phase, but in this case it's internal reflection so [tex]n_i=n_f[/tex] and I've read that for a change of phase in reflection, the transmitted material must have a higher refractive index than the incident one, which isn't the case in this exercise!).
I'm totally troubled and fail to understand what the heck is going on in this interesting exercise. Any help is greatly appreciated.
More details about the pic: I do not see any difference of intensity in any of the fringes of interference and they are equally distanced. Which lead me to think that the interference does not occur of the surface of the prism but I might be wrong. And sincerely I've never heard of such an interference where there's no difference of intensity in all fringes and suddenly the interference "stops" at a certain place. This problem was in my optics exam that I miserably failed.
P.S.: the direction of the rays in the sketch 1) is vertical. In 2), it wasn't indicated (hence my enormous confusion of where we see the interference!) but I'm guessing the rays should enter the page.