Optimal Paths: Comparing the Motion of Two Balls on Different Trajectories

[voko]

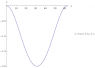
It can be shown that the lab-frame equations, in some normalized units, are: $$ x = ct - \sin t \\ y = 1 - \cos t, $$ where $t \in [0, 2 \pi ]$, $c > 1$, and where the units of time and length depend on $A, g$ and $V_0$. Attached is a lab-frame trajectory that I plotted with $c = 10$.

 

[haruspex]

haruspex (and possibly others) objected, reasoning that an inverted cycloid cannot possibly be a path "freely slidden upon" by a particle whose initial horizontal velocity is not zero, because such a path is vertical initially. That argument is flawed, however, because the inverted cycloid is the minimal time path in the initially comoving frame; in the lab frame where $V_0 \ne 0$, the minimal time path is the trajectory of the particle following a cycloidal path in the initially comoving frame; that path is not a cycloid per se.

Apologies - I had not understood what you giving as the solution. Yes, very neat - thanks.