Optimization Challenge - Poles and Wires

[MarkFL]

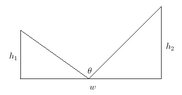
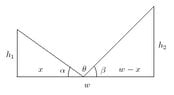
Suppose you have two poles separated by the distance $w$, the first of height $h_1$ and the second of $h_2$, where $0<h_1<h_2$. You wish to attach two wires to the ground in between the poles, one to the top of each pole, such that the angle subtended by the two wires is a maximum. What portion of the distance between the two poles, as measured from the first pole, must you take as the staking point for the two wires? Please refer to the following diagram:

View attachment 1101

 

[MarkFL]

solve (asin(x/a)+asin((1-x)/b))'=0 - Wolfram|Alpha

:p

and I should show that it's a maximum.

Sorry, but that is incorrect.

Also, I would prefer that work be shown, rather than simply relying on a CAS. The result should then be given in terms of $h_1,\,h_2,\,w$. (Sun)

 

[M R]

Sorry, but that is incorrect.

Also, I would prefer that work be shown, rather than simply relying on a CAS. The result should then be given in terms of $h_1,\,h_2,\,w$. (Sun)

Whoops. Sorry. It should have been atan of course.

I do do the maths on paper first by the way (usually). It's just easier to post a link to WA than it is to post a proper answer.

 

[MarkFL]

Whoops. Sorry. It should have been atan of course...

That was only one error...

edit: Perhaps not though...it depends on how you have defined $a$ and $b$.

 

[Opalg]

Here is an approach avoiding calculus.

View attachment 1102

​

If you draw a circle touching the ground and passing through the tops of the poles (at the points $P$ and $Q$) then it should be obvious geometrically that the wires should be attached at the point where the circle touches the ground.

Unfortunately, using this approach there does not seem to be an easy way to find the distance $x$ from the left pole to the point of attachment. The centre $C$ of the circle must lie on the perpendicular bisector of $PQ$, and the distance $CP$ must be equal to the height of $C$ above the ground. Using those facts, I found by some laborious calculations that $$x = \frac{\sqrt{h_1h_2\bigl(w^2 + (h_2-h_1)^2\bigr)} - h_1w}{h_2-h_1}.$$​

 

[MarkFL]

Very nice geometric method, Opalg! (Clapping)

My solution:

Spoiler

Please refer to the diagram:

View attachment 1104
We may state:

$$\alpha+\theta+\beta=\pi$$

$$\theta=\pi-(\alpha+\beta)$$

Now, we see that:

$$\tan(\alpha)=\frac{h_1}{x}$$

$$\tan(\beta)=\frac{h_2}{w-x}$$

Hence:

$$\theta=\pi-\left(\tan^{-1}\left(\frac{h_1}{x} \right)+\tan^{-1}\left(\frac{h_2}{w-x} \right) \right)$$

Differentiating with respect to $x$, we obtain:

$$\frac{d\theta}{dx}=-\frac{1}{1+\left(\frac{h_1}{x} \right)^2}\left(-\frac{h_1}{x^2} \right)-\frac{1}{1+\left(\frac{h_2}{w-x} \right)^2}\left(\frac{h_2}{(w-x)^2} \right)=$$

$$\frac{h_1}{x^2+h_1^2}-\frac{h_2}{(w-x)^2+h_2^2}=\frac{h_1\left((w-x)^2+h_2^2 \right)-h_2\left(x_2+h_1^2 \right)}{\left(x^2+h_1^2 \right)\left((w-x)^2+h_2^2 \right)}$$

Equating this to zero implies:

$$h_1\left((w-x)^2+h_2^2 \right)=h_2\left(x^2+h_1^2 \right)$$

Now, expanding and arranging in standard quadratic form, we obtain:

$$\left(h_2-h_1 \right)x^2+\left(2h_1w \right)x+h_1\left(h_1h_2-h_2^2-w^2 \right)=0$$

We find that the discriminant $\Delta$ is:

$$\Delta=\left(2h_1w \right)^2-4\left(h_2-h_1 \right)\left(h_1\left(h_1h_2-h_2^2-w^2 \right) \right)$$

After simplification we find:

$$\Delta=4h_1h_2\left(\left(h_2-h_1 \right)^2+w^2 \right)$$

and so, application of the quadratic formula on the quadratic in $x$, and discarding the negative root, there results:

$$x=\frac{-h_1w+\sqrt{h_1h_2\left(\left(h_2-h_1 \right)^2+w^2 \right)}}{h_2-h_1}$$

To find what portion of the distance between the two poles, as measured from the first pole, we must take as the staking point for the two wires, we may use:

$$\frac{x}{w}=\frac{-h_1w+\sqrt{h_1h_2\left(\left(h_2-h_1 \right)^2+w^2 \right)}}{w\left(h_2-h_1 \right)}$$