- #1
therest
- 25
- 0
Homework Statement
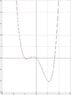
Find two points on curve y=x4-2x2-x that have a common tangent line.
Homework Equations
*the one stated above
dy/dx = 4x3-4x-1
The Attempt at a Solution
equation of a tangent line: y=mx+b
(4x3-4x-1) = m at two different points? So there are two points for which dy/dx=4x3-4x-1
I'm not sure what thinking I should be doing on this one to link the information about there being two points in the curve with the same tangent line to what I know about finding tangent lines. Will the coordinate points contain x or can I find two actual, definite points? Aren't there more than 2 places on the curve with the same tangent lines?