Optimization of the Area of a Triangle

[reigner617]

Homework Statement

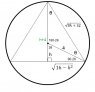
Find the area of the largest isosceles triangle that can be inscribed in a circle of radius 4. Solve by writing the area as a function of θ

Homework Equations

A=1/2 (bh)

The Attempt at a Solution

Given the side h and the hypotenuse 4, we can find the base of the smallest triangle to be sqrt(16-h²) which means that the base of the largest triangle is 2(sqrt(16-h²)). Its height can be considered as h+4, which would give a side length of sqrt(8h+32). So the area would be:
sqrt(16-h²)(h+4). However, they want it to be solved in terms of theta, which is the part that I am not sure of.

 

[BiGyElLoWhAt]

can you express h in terms of theta? express the sides of the triangle in terms of theta.

 

[reigner617]

for convenience, I'll say c= sqrt(8h+32). Would it be correct if I said the height was c(sinθ) and the base of the largest triangle 2c(cosθ)?

 

[LCKurtz]

I don't know where you got $c = \sqrt{8h+32}$. It would help if you labeled your picture. If you note that the angle between the two sides that you have labeled $4$ and $h$ is $2\theta$ that will help you get the two legs of that little right triangle in terms of $\theta$.

 

[reigner617]

If you note that the angle between the two sides that you have labeled 4 and h is 2θ

How did you determine that angle to be 2θ?
And to answer your question, I used the pythagorean theorem to find one of the side lengths

 

[RUber]

From what you have above, it seems that the height $(h+4)= Ccos(\theta)$ Where, as you mentioned, C is the length of the hypotenuse. You should be able to solve that for h in terms of theta and plug that into the formula for area.

 

[reigner617]

From what you have above, it seems that the height $(h+4)= Ccos(\theta)$ Where, as you mentioned, C is the length of the hypotenuse. You should be able to solve that for h in terms of theta and plug that into the formula for area.

If I solve for h, that would give me Ccosθ-4=h. Is it ok to have an extra variable (C) in there?

 

[LCKurtz]

How did you determine that angle to be 2θ?

That upper triangle is an isosceles triangle with equal sides of $4$. Its angles are $\theta,\theta, 180 -2\theta$. Label them. The supplement of that last one is the angle you are looking for.

Once you have that you have both $h$ and the other leg in terms of $\theta$.

 

[reigner617]

Are these labeled correctly?

If those are correct, can I use the law of sines such that

h/(sin90-2θ) = 4/sin90
h = 4(sin90-2θ)
h=4(1-2θ)
h=4-8θ

 

[LCKurtz]

Are these labeled correctly?
View attachment 74104
If those are correct, can I use the law of sines such that

h/(sin90-2θ) = 4/sin90

You mean $h/\sin(90-2\theta)$. Parentheses are important.

h = 4(sin90-2θ)
h=4(1-2θ)
h=4-8θ

Which is why you then get nonsense. Also, it is silly to use the law of sines given the picture. You have adjacent sides to the $h$ and $4$ for the angle $2\theta$. What trig function does that give you for $h$? Similarly for the other leg.

 

[reigner617]

That would be cos2θ=h/4
4cos2θ=h

 

[LCKurtz]

Yes. And what about the other leg?

 

[reigner617]

Well since h=4cos2θ, couldn't we just substitute it into the expression to get sqrt(16-(4cos2θ)^2) for the base?

 

[RUber]

That looks a lot like $4(\sqrt(1-\cos^2 2\theta)$. It seems like the long way to get to the opposite side from the angle $2\theta$ with hypotenuse 4.

 

[LCKurtz]

Well since h=4cos2θ, couldn't we just substitute it into the expression to get sqrt(16-(4cos2θ)^2) for the base?

Yes, you could, but you would want to simplify it. But, again, it is silly to do it that way. What trig formula uses opposite/hypotenuse?

 

[reigner617]

That would be sine. So if I were to use that, I would get sin(2θ)= [sqrt(16-(h^2))]/4. But I don't understand what this would accomplish since we're trying to look for max area, and that involves base and height

 

[reigner617]

Ahhh never mind. I think I see it now

 

[LCKurtz]

That would be sine. So if I were to use that, I would get sin(2θ)= [sqrt(16-(h^2))]/4. But I don't understand what this would accomplish since we're trying to look for max area, and that involves base and height

So instead of calling that leg $\sqrt{16-h^2}$ you can call it $4\sin(2\theta)$. Now you have both legs of that little triangle in terms of $\theta$. Now you can express the area of the original big triangle in terms of $\theta$. Then you are ready for the calculus problem of maximizing the area. Too bad the trig is holding you back so badly. Perhaps you should review it.

 

[reigner617]

So A= 1/2 (4cos(2θ))(4sin(2θ))
= 8cos(2θ)sin(2θ)

deriving this, we get A'= -16(sin(2θ))² + 16(cos(2θ))²

setting it to zero, we get θ= 30 degrees

substituting this for θ we get 2(sqrt(3))

However, another part of the question was solving the area in terms of h (I used A= [sqrt(16-h²)](h+4)

Following the same steps as I did for the one above, I get h=-4 and 2. h can't be -4 because if we use it, h+4 would go to zero, and the whole area would be zero. So h can only be 2.

Substituting this for h I get 12(sqrt(3))

What am I doing wrong?

 

[LCKurtz]

So A= 1/2 (4cos(2θ))(4sin(2θ))
= 8cos(2θ)sin(2θ)

Isn't the height of your triangle $4+4\cos(2\theta)$? And why the 1/2 out in front?

 

[reigner617]

Ah thank you for pointing that out. It works now. The 1/2 was put there by mistake because I was thinking fo 1/2 (bh). Thank you for all your help

 

[LCKurtz]

It works now? Given what I have seen so far, I doubt it. How about showing what you did to finish?

 

[reigner617]

I used 4cos(2x)+4 for the height so A=4sin2x(4+4cos2x). I derived that and still got 30 for the angle. Substituting that into the Area formula, I get 12(sqrt(3)) which is the same as the answer I got when I solved in terms of h

 

[RUber]

$4\sin 2\theta$ is 1/2 base and $4 + 4 \cos 2\theta$ is the height.
Your method of taking the derivative and setting it to zero is good. The best option is to rearrange the derivative as a quadratic function of $\cos 2 \theta$. h=-4 will be your minimum (zero) and another value for h will be your max. Both should be solutions of A'=0.

 

[LCKurtz]

I used 4cos(2x)+4 for the height so A=4sin2x(4+4cos2x). I derived that and still got 30 for the angle. Substituting that into the Area formula, I get 12(sqrt(3)) which is the same as the answer I got when I solved in terms of h

Good job. I presume you have noticed that the optimal shape is an equilateral triangle.