Optimizing Drumstick Bounce: Finding the Magic Fulcrum Point

[InTheWorks]

TL;DR Summary

The amount a drumstick bounces after hitting a surface depends on where you place the fulcrum along the stick. I'd like to understand why.

When a drummer holds a drumstick, the fingers form what's called a fulcrum. The stick pivots about this fulcrum. This question is not about striking from the hand with the drumstick. Instead, the drumstick is held horizontal and then allowed to fall due to gravity.

A drumstick has two ends. The tip is the end that strikes a surface. The other end is the butt end.

If you place the fulcrum at the centre of mass, the stick doesn't move when you let go of it (it's balanced). If you place the fulcrum on the tip side of the centre of mass and then let the stick go, the tip goes up instead of down as the butt end falls. If you place the fulcrum at the butt end of the stick, there is zero bounces. So for this work the fulcrum has to be somewhere between the centre of mass and the butt end of the drumstick.

There is a magic point somewhere between those two locations where the amount of bounce is maximum. A loose definition of maximum bounce is that the drumstick will have more bounces before coming to rest. Intuitively it feels like some aspect of rotation is balanced, but I don't know what.

This is not my pic, but it shows what the setup should look like:

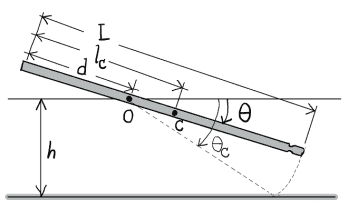
The centre of mass is at C. The pivot is at O.

A drum stick is an odd shape. A cylindrical rod works just as well and I did some testing with a piece of 1/2" dowel rod. Using the above picture as a reference:

$$L = 450mm$$
$$l_c = 225mm$$
$$d = 155mm$$

With $$d=155mm$$, there is maximum bounce. It may not be a coincidence that $$\frac{d}{l_c} \approx \frac{2}{3}$$.

The pic comes from a paper called "A simple mechanical model of the drumroll", but it develops a model for the time between bounces based on changing d, h, and the surface elasticity. I didn't grok anything in the derivation that answered my question.

 

[tech99]

The stick appears to be a compound pendulum, where its period depends on the pivot position. The period of the bounce mechanism, as with a trampoline, depends on amplitude. So I imagine the drummer adjusts the pivot position so that the period of the compound pendulum matches the period of the bounce at the particular amplitude he is using.

 

[Baluncore]

The effect will also depend on where the drum is struck. There are many possible modes of oscillation that can be excited in a membrane by an impulse. Think impedance matching. There will be sweet spots, and dead spots on the surface, that offer different reflection coefficients, to the drumstick configuration used.

 

[berkeman]

Instead, the drumstick is held horizontal and then allowed to fall due to gravity.

Not in my experience. You seem to be leaving out the spring forces involved.

Paging our resident professional drummer, @pinball1970

 

[pinball1970]

Not in my experience. You seem to be leaving out the spring forces involved.

Paging our resident professional drummer, @pinball1970

What a great thread to end the year on? Drums AND physics, fantastic.

Also, "Semi" professional, I have a day job ;)

I have thought about posting on this so many times but have never done it. Lots of physics going on.

So..

3/4 of the length is about right. If you approach the centre of the stick, gravity decreases because less of the mass is being pulled towards the head.

@Baluncore is also correct, dead centre of the head is dead, too near the rim is too taught so the head is not kicking back enough.
Around 3 inch out from centre is best.
In terms of terminology this will get messy, I learned drums before I understood any proper physics.

The more loose the head, the less the bounce, if you want to learn wrist control and build up all those ancillary muscles, you play your double stroke roll on a pillow, zero recoil.(an aside)

Holding the stick in the middle kind of seems logical but it does not work. Gravity bringing the stick down matched with muscles to initiate it. (Newton right now, ie a force rather than Einstein, although i can approach C if i am playing Purple)

Reason? You want the stick to go back down quickly if you want to play fast.
Small force down, gravity helps, relax, stick makes contact, recoil, muscle captures, muscle forces down again.

 

[pinball1970]

The stick appears to be a compound pendulum, where its period depends on the pivot position. The period of the bounce mechanism, as with a trampoline, depends on amplitude. So I imagine the drummer adjusts the pivot position so that the period of the compound pendulum matches the period of the bounce at the particular amplitude he is using.

I will upload something with varied positions so you can help me with this.

 

[InTheWorks]

I just wanted to clear up some confusion here.

This maximum bounce fulcrum position is purely a function of the stick. It will be in a different location on different sticks. It's not something the drummer adjusts to change the effect.

This is not playing a drum. It is simply determining the best place for the fulcrum on the stick given the constraint of maximum bounces.

Consider the surface a practice pad. This is a uniform, high rebound, gum rubber surface.

I looked up the compound pendulum and it seems like a good fit. However, there's lots of talk about radius of gyration and I haven't been able to understand that. I came across a patent for matching two wooden drum sticks that involved the radius of gyration so I feel that this is on the right track. Also that paper I mentioned used the radius of gyration.

The formula I keep seeing for the period of oscillation for a compound pendulum is:
$$ T = \frac{1}{2\pi}\sqrt{\frac{k^2 + h ^2}{gh}}$$

Where h is the distance from centre of mass to the pivot and k is the radius of gyration. I think maximizing this period is a good place to start. With $h^2$ in the numerator and $h$ in the denominator I'm not sure what to make of it.

If anyone wants to read that paper, it's here.

@pinball1970 playing on a pillow is where I'm headed with this question. Is that point of maximum bounce still the best place to hold the stick when there is no bounce? The application here is actually 'air drums'. If you haven't heard of Aerodrums before, it's a motion capture system that tracks drumstick. That's not this question though which I'd like to understand first.

If you want to see more about these 'air drum' strokes, there's some good content here

 

[pinball1970]

I just wanted to clear up some confusion here.

This maximum bounce fulcrum position is purely a function of the stick. It will be in a different location on different sticks. It's not something the drummer adjusts to change the effect.

This is not playing a drum. It is simply determining the best place for the fulcrum on the stick given the constraint of maximum bounces.

Consider the surface a practice pad. This is a uniform, high rebound, gum rubber surface.

I looked up the compound pendulum and it seems like a good fit. However, there's lots of talk about radius of gyration and I haven't been able to understand that. I came across a patent for matching two wooden drum sticks that involved the radius of gyration so I feel that this is on the right track. Also that paper I mentioned used the radius of gyration.

The formula I keep seeing for the period of oscillation for a compound pendulum is:
$$ T = \frac{1}{2\pi}\sqrt{\frac{k^2 + h ^2}{gh}}$$

Where h is the distance from centre of mass to the pivot and k is the radius of gyration. I think maximizing this period is a good place to start. With $h^2$ in the numerator and $h$ in the denominator I'm not sure what to make of it.

If anyone wants to read that paper, it's here.

@pinball1970 playing on a pillow is where I'm headed with this question. Is that point of maximum bounce still the best place to hold the stick when there is no bounce? The application here is actually 'air drums'. If you haven't heard of Aerodrums before, it's a motion capture system that tracks drumstick. That's not this question though which I'd like to understand first.

If you want to see more about these 'air drum' strokes, there's some good content here

What do mean by maximum bounce? The more force you provide the more bounce you get but that is not what good drummers do
Huge rebound is more difficult to control

 

[InTheWorks]

What I mean by maximum bounces is maximum number of bounces. For the same force (ie. just letting the tip of the stick drop from the same height), the stick will bounce more times when the pivot is in some places than others. This is because something, inertia perhaps, is resisting the rotational motion of the drumstick.

Everyone who learns drums for the first time does the same exercise. Once you learn how to hold the sticks in your hand and form a fulcrum, you drop it on the pad or drum to see where to put the fulcrum along the stick. It may not be done exactly the same way, for example, it might be done with a free stroke rather than dropping. Either way it's meant to do the same thing.

This effect is often described as letting the stick do the work.

It has nothing to do with the surface and nothing to do with the applied force. If you keep those things constant and vary the position of the fulcrum, the stick will bounce the most times when the fulcrum (pivot) is placed at the right spot. That's what I'm trying to understand. What determines that right spot?

 

[Baluncore]

It has nothing to do with the surface and nothing to do with the applied force. If you keep those things constant and vary the position of the fulcrum, the stick will bounce the most times when the fulcrum (pivot) is placed at the right spot. That's what I'm trying to understand. What determines that right spot?

The world of mechanical impedance matching is not that simple.
You are attempting to over simplify the problem.
For each point on the drum surface, there is an optimum fulcrum point on the stick.

 

[InTheWorks]

For each point on the drum surface, there is an optimum fulcrum point on the stick.

I've played on many different surfaces and I can tell you that the place where you get the most bounces of the tip of the drumstick is always at the same place on the stick. If it's changing at all, it's minute. It changes with different sticks (specifically different shapes that probably move the centre of mass), but not the surface.

If there are other factors at play, empirically, they aren't significant enough for me to notice. And you can take the drum surface completely out of the equation because I'm testing on either a solid surface (ie. a table) or a rubber practice pad. What I'm looking for is a property of the drumstick.

Intuitively, I would say that a stick 'weighs' the least if you place the pivot at the centre of mass. You should be able to make the stick change direction with the least input. Yet no one does this.

This might be because you can't play loud placing the pivot at the centre of mass. You also can't easily hit the centre of a 14" snare drum while also hitting the rim with a standard 16" drumstick. To play as loud as possible, you really need to hold the stick at the very end. At this location you don't get many bounces and the stick is feels heavy. I don't mean that it weighs alot. It's less lively.

There is something about the "weight" behind the pivot compared to the "weight" in front of the pivot that makes the stick behave differently. I say weight, but I mean some other quantity that I don't understand yet.

 

[Baluncore]

What I mean by maximum bounces is maximum number of bounces. For the same force (ie. just letting the tip of the stick drop from the same height), the stick will bounce more times when the pivot is in some places than others.

Most bounces will be when least damped, when the stick is matched to the surface.

And you can take the drum surface completely out of the equation because I'm testing on either a solid surface (ie. a table) or a rubber practice pad.

So you are matching the stick to the rubber practice pad, not to a real drum. That certainly makes it simpler.

There is something about the "weight" behind the pivot compared to the "weight" in front of the pivot that makes the stick behave differently. I say weight, but I mean some other quantity that I don't understand yet.

I believe that quantity is called mechanical or acoustic impedance. By changing the fulcrum position, you are scaling the impedance of the tip.

 

[InTheWorks]

I don't know what I'm doing here, but I went back to that paper which seems to be the closest thing to what I want to know. The thing that determines the bounce is the kinetic energy. From the paper:

We describe now the bounce of the stick
according to a simple inelastic collision model in
which the angular velocity ω i after the rebound is
expressed as a fraction α, to be interpreted as the
coefficient of restitution

It occurs to me that the highest bounce must also be the highest kinetic energy. The drawing again for easy reference.

Let's start with the kinetic energy
$$E_{kinetic} = \frac{1}{2}I_O\omega^2 $$
The paper derives the angular velocity as:
$$\omega(\theta) = \frac{1}{K_O}\sqrt{2g(l_c -d )\sin\theta} $$
Interestingly, $d = l_c$ means $\omega = 0$ regardless of $\theta$. The pivot at the centre of mass means it shouldn't fall. However, if $d \gt lc$ then there's a negative square root.

Another equation:
$$I_O=mK_O^2 $$
And I should be able to combine them:
$$E_{kinetic} = mK_O^2[\frac{1}{K_O}\sqrt{2g(l_c -d )\sin\theta}]^2 $$
$$E_{kinetic} = 2mg(l_c - d)\sin\theta $$
And that doesn't look right to me. If $d \geq l_c$ the kinetic energy is negative. If $d = l_c$ then the kinetic energy is zero. Based on this equation, the kinetic energy is highest when $d = 0$. That might be true, but the stick won't bounce when the pivot is at the butt end.

I found another equation in the paper that, using small angle approximation, says the acceleration is:
$$ \frac{d\omega}{dt} \approx \frac{(l_c-d)g}{K_O^2} $$

Now $K_O$ also depends on $d$:
$$K_O = \sqrt{\frac{2l_c}{3} -2l_cd + d^2} $$

That also came from the paper. Plugging it into the acceleration:
$$ \frac{d\omega}{dt} \approx \frac{(l_c-d)g}{\frac{2l_c}{3} -2l_cd + d^2} $$

I threw that equation into a graphing website (desmos) and it wasn't a function that had a maximum. So it's not peak acceleration either.

I guess I'll study that compound pendulum more next.

 

[A.T.]

View attachment 337955

Based on this equation, the kinetic energy is highest when $d = 0$. That might be true, but the stick won't bounce when the pivot is at the butt end.

Can the deformation of the sick play the key role, at least when hitting a harder type of percussion? lt seems that for $d = 0$ the stick deformation would just be a standing wave with two nodes at the ends, so not much amplitude and thus "kick back" at the tip. But with a free butt end you get different wave dynamics, which for some $d$ maximize the amplitude at the tip.

 

[InTheWorks]

Can the deformation of the sick play the key role, at least when hitting a harder type of percussion? lt seems that for $d = 0$ the stick deformation would just be a standing wave with two nodes at the ends, so not much amplitude and thus "kick back" at the tip. But with a free butt end you get different wave dynamics, which for some $d$ maximize the amplitude at the tip.

This is a good thought, but I don't know how I can prove or disprove it. Any suggestions to test or model it?

I built a model from Lego and the effect is there too. The Lego piece I used is a long beam with holes in it so I can position the pivot in different places. It is 96mm long. It has 11 holes and one smack dab in the middle. The height from the pivot to the ground is 34mm. The pivot is an axle piece passing through two lego blocks and the beam.

Some observations:
1. the hard countertop surface I taped the base to was not producing much bounce. I taped a piece of broken balloon at the contact point and this helped. It's not surprising.

2. a drumstick bounces just fine on the same countertop.

3. there is a sweet spot on the Lego model located at hole 4 from the butt end. That's 32mm of the 96mm. That's also 1/3 of the length.

4. when the pivot is at the last hole at the butt end, it doesn't bounce. However, if the beam is dropped from higher than horizontal, it can bounce a little.

5. when the pivot is at the centre hole, it doesn't bounce when dropped. However, if the beam is flicked it will bounce back up.

Some thoughts about the stick bounces:

1. a function of the energy returned from the collision.
2. a function of the weight forward of the pivot and maybe the weight behind the pivot.
3. the 1/3 length requires the least energy to move the stick upward after a collision

There needs to be enough energy returned from the collision to overcome some kind of inertia. The rotation is about the pivot so that inertia should just be it. That inertia just increases the farther you go from the centre. But perhaps there is non rotational inertia involved very briefly at the moment of collision?

It feels like the geometry matters. Moving the pivot changes the contact angle. The angle at the pivot changes from $22^\circ$ at the butt end, to $32^\circ$ at the sweet spot, and to $44^\circ$ at the centre hole. As a result, the amount of force normal to the contact point is going to be different depending on the angle.

Somehow these two effects are combining to produce a system minimum.

I could also hold the model up vertically, like a pendulum. What I discovered there is that the pendulum swings most when the pivot is at the butt end. When it's at the 'sweet spot' for the most bounces, the pendulum swings less. When the pivot is placed at the centre hole, the pendulum doesn't swing at all. It's not surprising, but I think it rules out any kind of simple harmonic motion.

 

[A.T.]

This is a good thought, but I don't know how I can prove or disprove it. Any suggestions to test or model it?

I built a model from Lego and the effect is there too. The Lego piece I used is a long beam with holes in it so I can position the pivot in different places.

I would try something much longer and less stiff (but as elastic as possible). That would increase the magnitude of the deformation and reduce the frequencies, so it would be easier to observe at video frame rates video that consumer grade devices offer.

 

[InTheWorks]

I played with the height of my model. The total height difference at the pivot from lowest to highest was 28.8mm. Here are my observations:

1. more height gives higher bounces (there is more potential energy to start)
2. with more height the sweet spot may move from hole 4 to between holes 3 and 4.

At lower heights it's obvious that hole 4 is better than hole 3, but as the height goes up it becomes harder to tell between the two. I don't have a measurement for the amount of bounces. I'm using my ear to hear the number of bounces. It's very subjective, but I don't have a good setup to test this.

If I don't tape the base down the reaction forces are moving the whole model. Now I'm wondering if there's anything to learn from the reaction forces?

 

[InTheWorks]

I would try something much longer and less stiff (but as elastic as possible). That would increase the magnitude of the deformation and reduce the frequencies, so it would be easier to observe at video frame rates video that consumer grade devices offer.

Much longer will change the deflection if the section doesn't change. A wimpy section would be a thin rod. It needs to be stiff enough to not deform appreciably upon contact so not too thin of a rod. Elastic as possible means high Young's modulus. So steel?

The problem I'm seeing is that I've now turned the beam into a spring.

 

[A.T.]

Elastic as possible means high Young's modulus. So steel?

Not stiff, but low energy dissipation.

The problem I'm seeing is that I've now turned the beam into a spring.

Every beam is a spring too.

 

[InTheWorks]

In case anyone wants to see what I'm talking about, here's a youtube video that I happened upon (I couldn't find it when I was looking):

 

[InTheWorks]

Not stiff, but low energy dissipation.

I have no idea what kind of material you're suggesting.

But then I thought, what if we go the other way? There are drumsticks made of a few materials: maple, hickory, oak, aluminum, and carbon fibre. The drumsticks should be soft compared to the cymbals they hit. The aluminum drumsticks have a plastic sleeve that takes damage and needs replacement.

I only have maple and hickory sticks. They both do the same thing. I watched a bunch of reviews on aluminum and carbon fibre sticks and they do the same thing too with respect to this bouncing that's hard to define. I don't know how these materials fit to your not stiff, but low energy dissipation requirement. Probably not a match? Probably not long enough either.

Stiffness is a function of the geometry and elastic modulus. So we can get there a number of ways. Low stiffness implies deflection. If the material has a elastic modulus, it won't dissipate energy with deflection. Unlike viscous or elastomeric materials. Neither of which I would call stiff.

For a given stiffness, enough load will cause deflection. Or going the other way, given a load we can find a stiffness that will cause the required deflection.

So not stiff, but still low energy dissipation. To me that means low stiffness by geometry and high elastic modulus.

 

[InTheWorks]

My question has been asked before on this forum without an answer.

This answer was not vetted or accepted. It talks about the centre of percussion.

This is the reverse of the situation of where to hit a baseball along the length of the bat.

In that situation, the sweet spot is where the strike on the bat displaces it (bends it) to set up the simplest of wave motion of the bat - the strike point being the single node with the portion of the bat before and beyond the strike point taking taking part in a single curve... this is the elastic deformation that provides the most force back to the ball.

For the drummer, the same applies in reverse - he wants to hold the stick at the point where hitting the drumhead causes the simplest deformation of the stick, flexing forward and behind the node where he holds it, each flex being half of an "s" curve.

I don't have a baseball bat, but I have a pool noodle. And guess what. It behaves like drumstick. There is a sweet spot where there are more bounces. It's just stiff enough to not deflect horribly with gravity. I can see it deflect on impact, but honestly I can't tell if the deflection is any different at the sweet spot vs holding it at the end.

It sounds like this centre of percussion is what @A.T. was getting at?

It would seem like this centre of percussion is indeed the phenomenon behind drumstick bounce. I will do some more research.

 

[A.T.]

This answer was not vetted or accepted. It talks about the centre of percussion.

I agree with @bahamagreen that the center of percussion problem is the drumstick pivot question in reverse: you optimize the impact location for a given pivot, instead of pivot for a given impact location. The less reactive force your hand has to apply on impact, the less energy dissipation you have, because your hand is not very elastic (has lots of damping and dissipation).

Here is a very simple analysis to find that optimal pivot:

Consider a uniform beam floating in space, and being hit by a short impulsive perpendicular force at one end. The instantaneous linear acceleration is:

$a = F /m$

While the instantaneous angular acceleration is:

$\alpha = \tau / I = F/m \cdot 6/L$

So their ratio is:

$a/\alpha = L/6$

Which means that the instantaneous center of rotation (stationary point) will be $L/6$ away from the center of mass, opposite to the impact end. That is the optimal pivot for a rigid uniform beam.

It sounds like this centre of percussion is what @A.T. was getting at?

Previously I was rather speculating about the deformation of the object having an impact, which is not considered in the center of percussion derivation or my simple analysis above. It is an additional factor, but I don't know how relevant it is for a drumstick. From the wiki page:

"The center of percussion defines a place where, if the bat strikes the ball and the batter's hands are at the pivot point, the batter feels no sudden reactive force. However, since a bat is not a rigid object the vibrations produced by the impact also play a role."

 

[InTheWorks]

Which means that the instantaneous center of rotation (stationary point) will be $L/6$ away from the center of mass, opposite to the impact end. That is the optimal pivot for a rigid uniform beam.

If the centre of mass is at $\frac{L}{2}$ and I add $\frac{L}{6}$ I get $\frac{2}{3}L$. That's what the normal centre of percussion calculation would produce for a uniform beam with a pivot at one end. Interesting.

The problem I have with these analyses, is that they don't make any prediction about why the stick would bounce most if the pivot is placed at the centre of percussion. In what way is that pivot location optimal for the number of bounces? Is it because less energy goes into moving the stick in directions other than rotation about the pivot?

I've definitely been looking at this wrong. The starting diagram should be with the stick tip at an angle already in contact with the surface. From here the surface applies an impulse to the stick tip. Now it becomes a question of how to maximise the height of the tip for any impulse. Or rather maximise the potential energy as it comes to a stop.

Previously I was rather speculating about the deformation of the object having an impact, which is not considered in the center of percussion derivation or my simple analysis above. It is an additional factor, but I don't know how relevant it is for a drumstick.

It could be relevant for drum strokes that have more force behind them. In this example of dropping the stick from horizontal, I'm not so sure. That paper I mentioned before got some good correlation between how many times the drumstick bounced in simulation vs experiment when falling from horizontal due to gravity.

 

[A.T.]

In what way is that pivot location optimal for the number of bounces?

The less reactive force your hand has to apply on impact, the less energy dissipation you have, because your hand is not very elastic (has lots of damping and dissipation).

 

[Baluncore]

I've definitely been looking at this wrong. The starting diagram should be with the stick tip at an angle already in contact with the surface. From here the surface applies an impulse to the stick tip. Now it becomes a question of how to maximise the height of the tip for any impulse. Or rather maximise the potential energy as it comes to a stop.

I think you should investigate the short time, while the tip of the stick is in contact with the membrane. If the tip contact time is longer, there will be less high frequency sound generated, that would waste energy. To lengthen the duration of contact, match the impedance of the tip to the impedance of the membrane.

 

[InTheWorks]

The less reactive force your hand has to apply on impact, the less energy dissipation you have, because your hand is not very elastic (has lots of damping and dissipation).

Let's take the hand out of the equation. The Lego model I built does the same thing and there is no hand to dampen or dissipate.

Earlier you wrote that the angular acceleration was:
$$\alpha = \frac{\tau}{I} = \frac{F}{m} \frac{6}{L}$$
I've been picking my brain trying to understand how that comes to be.

Questions:
1. why does the angular acceleration depend on the linear acceleration like that?
2. where does the $\frac{6}{L}$ come from?

Yeah basically I can't understand any of it.

 

[InTheWorks]

I have been giving this a lot of thought. The reason for a specific pivot to yield the most number of bounces must have something to do with the angular velocity at impact.

I tried looking for that before, but I think I made a mistake. The first mistake was equating kinetic to potential energy as written in the paper. The equation in paper for potential energy is:
$$E_{potential} = mg(l_c - d)$$
I think, perhaps, there is a missing $\sin\theta$. Because $l_c-d$ becomes the hypotenuse of a right angle triangle (from the pivot to the centre of mass) with respect to the original horizontal position. So the total distance that the centre of mass fell is:
$$E_{potential} = mg(l_c - d)\sin\theta$$
Now, can set that equal to kinetic energy:
$$ E_{kinetic} = I\omega^2 = mK_0^2\omega^2 = mg(l_c - d)\sin\theta$$
and rearrange for $\omega$:
$$\omega = \frac{1}{K_O}\sqrt{g(l_c - d)\sin\theta} $$
If I put that into desmos, there is a maximal value over $\theta$ as $d$ changes.

One more simplification will change the final angular velocity into purely a function of $d$. $\omega$ at the start is 0 and $\omega$ will be maximum at the angle where the tip contacts the surface. That angle is $\sin\theta = h/(L - d)$ where $h$ is the height of the pivot and $L-d$ is the length of the stick below the pivot.
$$\omega_{final} = \frac{1}{K_O}\sqrt{\frac{gh(l_c - d)}{(L - d)}} $$
The final form for the final angular velocity as a function of $d$ is:
$$\omega_{final} = \frac{\sqrt{\frac{gh(l_c - d)}{(L - d)}}}{\sqrt{\frac{L^2}{3} + d^2 -Ld}} $$
I can graph that and find out that the maximum final angular velocity occurs when $d = 0.12m$ for $L=0.4m$ with a rather coarse step size. The ratio of d/L is 0.3. If I try to narrow down the value of $d$, it gets smaller. That means it's less than 1/3 which does not match the centre of percussion exactly.

 

[A.T.]

Let's take the hand out of the equation. The Lego model I built does the same thing and there is no hand to dampen or dissipate.

Any real world pivot is not 100% ideal. Under impulsive forces it will deform, move and dissipate some energy. Minimizing the impulsive forces at the pivot, minimizes the energy dissipated directly at the pivot for any type of real world pivot.

However, even an ideal pivot that doesn't dissipate energy by itself, might affect the stick deformation dynamics and the bouncing behavior. But this is not considered at this simple level of analysis.

Earlier you wrote that the angular acceleration was:
$$\alpha = \frac{\tau}{I} = \frac{F}{m} \frac{6}{L}$$
I've been picking my brain trying to understand how that comes to be.

https://en.wikipedia.org/wiki/List_of_moments_of_inertia

$$\alpha = \frac{\tau}{I} = \frac{F\frac{L}{2}}{\frac{1}{12}mL^2} = \frac{F}{m} \frac{6}{L}$$

 

[A.T.]

The reason for a specific pivot to yield the most number of bounces must have something to do with the angular velocity at impact.

Without energy dissipation, any angular velocity on impact will be fully retrieved, and the stick will bounce forever. So the rate of energy dissipation is key here, while you are just looking at the initial energy.

To see what matters more you can do some experiments:

Compare the bounce times for different drop heights (and thus initial energies), but the same pivot location. Repeat for different pivot locations.

Or approach it theoretically:

Energy dissipation in bouncing is often modeled as an exponential decay:
https://en.wikipedia.org/wiki/Exponential_decay
You can compare how much the different initial energies (for d = 0.3 vs 1/3) affect the time to dissipate most of the initial energy (like 99%), and then compare that to observation, and to how much the result is affected by the dissipation rate (which can vary greatly based on the impulsive forces the lossy pivot has to counter).

 

[InTheWorks]

$$\alpha = \frac{\tau}{I} = \frac{F\frac{L}{2}}{\frac{1}{12}mL^2} = \frac{F}{m} \frac{6}{L}$$

Thank you. The additional step in between makes it crystal clear.

 

[DaveC426913]

Not gonna lie, this honestly what i was expecting when I clicked through.

(Add vectors and numbers to-taste. I dont have Photoshop on me.)

The more loose the head, the less the bounce, if you want to learn wrist control and build up all those ancillary muscles, you play your double stroke roll on a pillow, zero recoil.(an aside)

Loosely related. I tried playing a bit. I could never figure out to achieve a bass drum beat. The pedal would kick back too fast and aggressively, ruining the rhythm. Probably me being too timid.

But maybe it would be best to cleave off a thread about general drum physics.