- #1
bobsmith76
- 336
- 0
These are the contents of the books I'm going to be reading to prepare myself for Quantum Mechanics. I was wondering if there any chapters that are not really necessary to learn. For instance, in studying Calculus it seems unlikely to me that infinite series will every be useful, though I might be wrong. I would like to eventually try Particle Physics, Nuclear Physics and Quantum Field Theory and a few basic of String Theory, so if there is some math in these books that is not needed for QM but is needed for the other physics then I should study that too. All this is for my own personal enjoyment and I'm studying it not because I want to be a physicist but because I want to understand the math behind the Big Bang, Cosmology, the Multiverse and the Fine-Tuning Argument.
Also I realize that more math is needed for physics beyond QM. I'm not worried about that now.


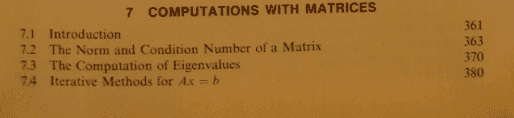






Also I realize that more math is needed for physics beyond QM. I'm not worried about that now.
