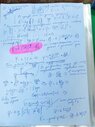Optimizing Polar Axis for Dipole in Polar Coordinates

[DaraRychenkova]

Homework Statement

- Determination of the dipole (p=ql). Find the dipole potential at a distance r much larger than the size of the dipole itself. Calculate the field of the dipole using the relationship between the potential and the field.



1. Solve the problem of finding the dipole field using the expression for the potential obtained in the previous problem in polar coordinates

Relevant Equations

Dipole, electrostatic

I don't know how to get the result referring to the previous task. Is my decision correct?

 

[kuruman]

The potential in the "previous problem" is probably something like $$V=\frac{1}{4\pi\epsilon_0}\frac{\mathbf{p}\cdot\mathbf{r}}{r^3}.$$ If it is in some other form, use that. What do you think "the relationship between the potential and the field" is?

 

[vanhees71]

I can't make sense of the posted scan. Obviously you've given the electric field in coordinate-free notation,
$$\vec{E}=\frac{1}{4 \pi \epsilon_0 r^5}(3 \vec{r} \vec{r} \cdot \vec{p}-r^2 \vec{p}).$$
Now first think about, how to choose your polar axis. With the right choice, it's very quickly solved!