Ph4cm
- 6
- 0
A truck traveling interstate, driving at a constant speed of 110km/h, gets 7km/L efficiency and loses 0.1km/L in fuel efficiency for each km/h increase in speed. Costs include diesel ($1.49/L), truck drivers’ wage ($35/hour), and truck maintenance and repairs ($9.50/hour). This truck is mainly used for carrying freight between Adelaide and Sydney (1375km). Explain what would happen if the truck were able to maintain a constant speed over 250km/h?
Is it reasonable to assume a constant speed for such a trip?
(Find 2 sources)
What factors affect the reasonableness of the model the most?
Suppose that, for every extra freight container the truck carries, the fuel efficiency drops by 0.05km/L. Suggest what will happen to the optimum traveling speed as the load of the truck’s freight increases.
Find a mathematical relationship between freight size and speed for which cost is a minimum. Discuss your findings.
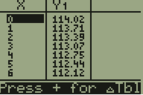
I've figured out the cost model C= 1375*(801-2.96x)(x(18-0.1x)) (x is speed, C is total cost)
Is it reasonable to assume a constant speed for such a trip?
(Find 2 sources)
What factors affect the reasonableness of the model the most?
Suppose that, for every extra freight container the truck carries, the fuel efficiency drops by 0.05km/L. Suggest what will happen to the optimum traveling speed as the load of the truck’s freight increases.
Find a mathematical relationship between freight size and speed for which cost is a minimum. Discuss your findings.
I've figured out the cost model C= 1375*(801-2.96x)(x(18-0.1x)) (x is speed, C is total cost)