- #1
stunner5000pt
- 1,461
- 2
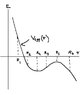
attached is the effective potential plotted on E vs r graph. Discuss the nature of the orbits are the various values for r
also [tex] V_{eff} (r) = - \frac{\alpha}{r} - br^2 - \frac{L^2}{2mr^2} [/tex]
where b << alpha
L is the angular momentum and is not zero
for R > R5 the orbit is a hyperbola because the value of r will go on increasing infinitely
for R2 <= R <= R3 the orbit is an ellipse because the orbit is bounded
for R = R4 or R = R5 then the orbit is a circle special case where there is no external torque
for R< R1 orbit is a parabola? (not sure)
im not usre how to interpret R = 0 and R1< R < R2
also [tex] V_{eff} (r) = - \frac{\alpha}{r} - br^2 - \frac{L^2}{2mr^2} [/tex]
where b << alpha
L is the angular momentum and is not zero
for R > R5 the orbit is a hyperbola because the value of r will go on increasing infinitely
for R2 <= R <= R3 the orbit is an ellipse because the orbit is bounded
for R = R4 or R = R5 then the orbit is a circle special case where there is no external torque
for R< R1 orbit is a parabola? (not sure)
im not usre how to interpret R = 0 and R1< R < R2