- #1
yazz912
- 45
- 0
1. The problem statement, all variables and given/known
Show that
∫∫∫ 12y^2 z^3 sin[x^4] dxdydz
Region: { y< x< z
0< y< z
0 <z< (Pi)^ 1/4
Equals Pi/4
Change order of integration to dydxdz 2. Homework Equations
Order of integration
3. The Attempt at a Solution
First I graphed my region on the on the zy- plane and then I graphed my region on the xz- plane . I know my limits of integration for z will not change bc I'm still going from 0 to (Pi)^1/4
And as far as my limits for dy I have to put it in terms of x and z.
But I'm not seeing what my limits are to convert to dydxdz.
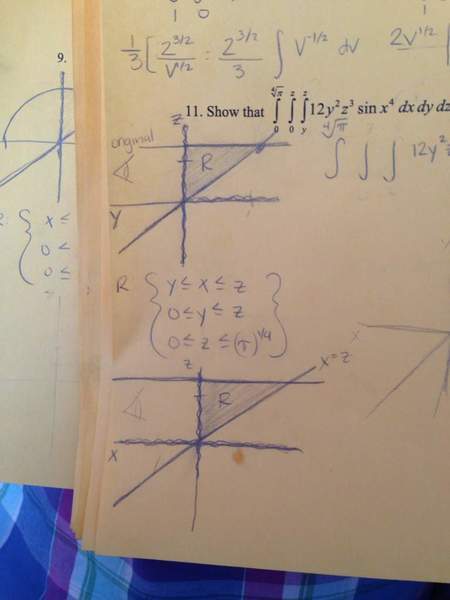
Show that
∫∫∫ 12y^2 z^3 sin[x^4] dxdydz
Region: { y< x< z
0< y< z
0 <z< (Pi)^ 1/4
Equals Pi/4
Change order of integration to dydxdz 2. Homework Equations
Order of integration
3. The Attempt at a Solution
First I graphed my region on the on the zy- plane and then I graphed my region on the xz- plane . I know my limits of integration for z will not change bc I'm still going from 0 to (Pi)^1/4
And as far as my limits for dy I have to put it in terms of x and z.
But I'm not seeing what my limits are to convert to dydxdz.