Order of rotations: precession, nutation, spin

[Trying2Learn]

TL;DR Summary

What is the order of the rotations

Hello

I attach a picture of a problem from a dynamics textbook.

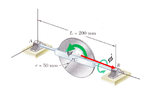
The axle rotates about the axis AB

WHILE (and the "while" here is a significant word to my question) it does that, the disk spins about an axis through C, but perpendicular to the face of the disk.

As the textbooks solve problems like this (and, in this example, despite the title of this post, there is no nutation, but an induced moment -- which is not relevant to this question), they state that the FIRST rotation is the one about AB. Then, AFTER that, we have the spin.

My question is: why that order?

Can one solve the problem by first modeling the body spin, and then, after that, the axle spin?

I can relate this to the subject line, by asking "how do we KNOW that the order of rotations in gyroscope is: precession, nutation, spin?"

-------------------------

Actually, I will answer this myself (I just took the time to think).

If I modeled the spin first, then the LOCAL axis of that body (AB) would no longer be along AB, but it will have spun. Then, it will be a different problem.

OK, I can see that. But I used this problem because the bigger issue for me is the order of rotations in the gyroscope. So, for a gyro, why do we model the rotations in that order (spin of the body being last)?

 

[BvU]

Can one solve the problem

What problem ?

 

[vanhees71]

The problem seems to be the strange idea there was "an order of rotations". A top is most simply seen as a rigid body which is free to rotate around a fixed point (which is not exactly the problem according to the attached figure, which is more restricted, but it's good to understand the simple case first, and it's not simple at all anyway). It's motion is of course a rotation around the point, and it is described by three degrees of freedom. To understand this note that the momentary rotation can be described by a unit vector $\vec{n}$ defining the momentary axis of rotation and the rotation angle around this axis. For the unit vector you need two angles to describe its location relative to the space-fixed coordinate system. So all together you have three degrees of freedom of rotation. There is just this momentary rotation but no "order of rotations".

For a very thorough and as elementary as possible treatment of the spinning top, see

A. Sommerfeld, Lectures on Theoretical Physics, Vol. 1 (Mechanics).

 

[Trying2Learn]

The problem seems to be the strange idea there was "an order of rotations". A top is most simply seen as a rigid body which is free to rotate around a fixed point (which is not exactly the problem according to the attached figure, which is more restricted, but it's good to understand the simple case first, and it's not simple at all anyway). It's motion is of course a rotation around the point, and it is described by three degrees of freedom. To understand this note that the momentary rotation can be described by a unit vector $\vec{n}$ defining the momentary axis of rotation and the rotation angle around this axis. For the unit vector you need two angles to describe its location relative to the space-fixed coordinate system. So all together you have three degrees of freedom of rotation. There is just this momentary rotation but no "order of rotations".

For a very thorough and as elementary as possible treatment of the spinning top, see

A. Sommerfeld, Lectures on Theoretical Physics, Vol. 1 (Mechanics).

Thank you!