Orthogonal trajectories of curves

Click For Summary

Discussion Overview

The discussion revolves around finding the orthogonal trajectories of two sets of curves defined by the equations \(x^{2}-y^{2}=c\) and \(x^{2}+y^{2}+2cy=1\). Participants explore the mathematical methods to derive these trajectories, including differential equations and graphical interpretations.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant presents their findings for the curves and seeks confirmation on their correctness and next steps.
  • Another participant agrees with the initial findings but suggests a refinement regarding the parameter \(D\) in the second equation.
  • Concerns are raised about the necessity of finding a commonality between the two sets of solutions, with one participant asserting they are separate questions.
  • A later reply challenges the correctness of the proposed solution for the second set of curves, arguing that the lines are only orthogonal at specific points defined by \(c\) and that a more general solution is needed.
  • The same participant provides a detailed derivation of a differential equation to eliminate \(c\) and proposes that the orthogonal curves are actually circles centered on the y-axis, rather than lines.
  • Another participant expresses understanding after the clarification and thanks the contributor for the insights.

Areas of Agreement / Disagreement

Participants express differing views on the nature of the solutions for the second set of curves, with some asserting they are lines while others argue they are circles. The discussion remains unresolved regarding the orthogonal trajectories, as multiple interpretations exist.

Contextual Notes

There are unresolved mathematical steps and assumptions regarding the parameter \(c\) and its implications on the solutions. The discussion reflects varying interpretations of the relationships between the curves and their orthogonal trajectories.

evinda
Gold Member
MHB
Messages
3,741
Reaction score
0
Hello !
I have to find the orthogonal trajectories of the curves :

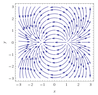
x^{2}-y^{2}=c , x^{2}+y^{2}+2cy=1 ..

How can I do this??

For this: x^{2}-y^{2}=c I found \left | y \right |=\frac{M}{\left | x \right |} ,and for this: x^{2}+y^{2}+2cy=1,I found: y=Ax-D,c,A,D \varepsilon \Re .

Is this right??And how can I continue??
 
Physics news on Phys.org
evinda said:
Hello !
I have to find the orthogonal trajectories of the curves :

x^{2}-y^{2}=c , x^{2}+y^{2}+2cy=1 ..

How can I do this??

For this: x^{2}-y^{2}=c I found \left | y \right |=\frac{M}{\left | x \right |} ,and for this: x^{2}+y^{2}+2cy=1,I found: y=Ax-D,c,A,D \varepsilon \Re .

Is this right??And how can I continue??

Hi evinda! :D

That is right enough.
Actually, you can sharpen the second one a bit since $D=c$.

What do you want to continue with?
Aren't you already done?
 
I like Serena said:
Hi evinda! :D

That is right enough.
Actually, you can sharpen the second one a bit since $D=c$.

What do you want to continue with?
Aren't you already done?

Since both of the curves are given at the same subquestion,don't I have to find something common between those two solutions?? :confused: Or,what do I have to do?? :confused:
 
evinda said:
Since both of the curves are given at the same subquestion,don't I have to find something common between those two solutions?? :confused: Or,what do I have to do?? :confused:

The solution for the first set of curves is a set of hyperboles.
The solution for the second set of curves is a set of lines.
They have nothing in common.
So in my opinion they are separate questions and your answer is sufficient.
 
I like Serena said:
The solution for the first set of curves is a set of hyperboles.
The solution for the second set of curves is a set of lines.
They have nothing in common.
So in my opinion they are separate questions and your answer is sufficient.

Nice..Thank you very much! :)
 
Hold on! :o

Something was still bugging me about that $c$ in the second set of curves $$x^2+y^2+2cy=1 \qquad (1)$$
When I started to draw them, I realized that
$$y=Ax-c \qquad \qquad (2)$$
is not the proper solution.
Draw them. You'll see!Those lines are only orthogonal for points on 1 specific circle that is defined by $c$.
To find the curves that are orthogonal to the whole set of circles, we need to eliminate $c$.

From (1), we get that:
\begin{array}{}
\frac{x^2}{y}+y+2c&=&\frac 1 y \\
\frac{2x}{y}dx - \frac{x^2}{y^2}dy + dy + 0 &=& -\frac{1}{y^2}dy \\
2xydx&=&(x^2-y^2-1)dy
\end{array}
See, no $c$ involved anymore! ;)
The solution of this differential equation is the set of curves (actually circles with their center on the y axis) in (1).
View attachment 1702

To find the orthogonal curves, we need to solve the "orthogonal" differential equation:
\begin{array}{}
(x^2-y^2-1)dx&=&-2xydy \\
\Big(1 - \frac{y^2}{x^2} - \frac 1 {x^2} \Big)dx &=& - \frac{2y}{x}dy \\
dx + \left(- \frac{y^2}{x^2}dx + \frac{2y}{x}dy \right) - \frac 1 {x^2}dx &=& 0 \\
x + \frac{y^2}{x} + \frac{1}{x} &=& 2C \\
x^2 + y^2 - 2Cx &=& -1 \\
(x - C)^2 + y^2 &=& C^2 - 1
\end{array}
In other words, this is a set of circles (with their center on the x-axis) instead of a set of lines.
View attachment 1703
 

Attachments

  • x2+y2+2cy=1.png
    x2+y2+2cy=1.png
    11.6 KB · Views: 103
  • orthogonal_x2+y2+2cy=1.png
    orthogonal_x2+y2+2cy=1.png
    11.6 KB · Views: 103
I like Serena said:
Hold on! :o

Something was still bugging me about that $c$ in the second set of curves $$x^2+y^2+2cy=1 \qquad (1)$$
When I started to draw them, I realized that
$$y=Ax-c \qquad \qquad (2)$$
is not the proper solution.
Draw them. You'll see!Those lines are only orthogonal for points on 1 specific circle that is defined by $c$.
To find the curves that are orthogonal to the whole set of circles, we need to eliminate $c$.

From (1), we get that:
\begin{array}{}
\frac{x^2}{y}+y+2c&=&\frac 1 y \\
\frac{2x}{y}dx - \frac{x^2}{y^2}dy + dy + 0 &=& -\frac{1}{y^2}dy \\
2xydx&=&(x^2-y^2-1)dy
\end{array}
See, no $c$ involved anymore! ;)
The solution of this differential equation is the set of curves (actually circles with their center on the y axis) in (1).
View attachment 1702

To find the orthogonal curves, we need to solve the "orthogonal" differential equation:
\begin{array}{}
(x^2-y^2-1)dx&=&-2xydy \\
\Big(1 - \frac{y^2}{x^2} - \frac 1 {x^2} \Big)dx &=& - \frac{2y}{x}dy \\
dx + \left(- \frac{y^2}{x^2}dx + \frac{2y}{x}dy \right) - \frac 1 {x^2}dx &=& 0 \\
x + \frac{y^2}{x} + \frac{1}{x} &=& 2C \\
x^2 + y^2 - 2Cx &=& -1 \\
(x - C)^2 + y^2 &=& C^2 - 1
\end{array}
In other words, this is a set of circles (with their center on the x-axis) instead of a set of lines.
View attachment 1703

I understood it now :o Thank you very much! :)
 

Similar threads

Undergrad What are the applications of inverses of vector functions?
  • · Replies 17 ·
Replies
17
Views
3K
MHB What are the orthogonal trajectories of e^{x}(xcosy - ysiny) = c?
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Limit cycles, differential equations and Bendixson's criterion
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Direction Fields and Isoclines
  • · Replies 1 ·
Replies
1
Views
814
Undergrad Determining equilibrium solutions to differential equations
  • · Replies 16 ·
Replies
16
Views
3K
Undergrad 2nd order ODE's, variation of parameters and the notorious constraint
  • · Replies 5 ·
Replies
5
Views
2K
MHB B.2.2.16 IVP of \dfrac{x(x^2+1)}{4y^3}, y(0)=-\dfrac{1}{\sqrt{2}}
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad 1D time dependent PDE - using orthogonal collocation
  • · Replies 2 ·
Replies
2
Views
4K
Undergrad Using v substitution for first order homogenous DE and constraining solution
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad How to do Magnus expansion for time-dependent companion matrix?
  • · Replies 7 ·
Replies
7
Views
3K