charie
- 3
- 0
- Homework Statement
- it was assigned as by the lecturer.
- Relevant Equations
- conservation of energy
[Mentor Note: Two duplicate threads merged...]
in container with dimensions L×D, rests water of height H and density ρ. we disturb the water along L dimension, and accept an oscillation is caused on the free surface of the water, which maintains its flatness, so that the central of mass of the water moves up-down and left-right, and the water does not move in the extreme positions but only has change in potential energy due to gravity, while in the middle positions where the surface is horizontal, all the energy gets converted to kinetic energy. say the central of mass is in position ##(x_o,y_o)## in equilibrium, and ##(x,y)## during the oscillation. how do we show that ##mg(y-y_o)## is proportional to ##(x-x_o)^2##, and find cyclic frequency of the oscillation of the water?
i have tried to prove said proportionality using conservation of energy as follows: for every column of height ##(H+a)##, it is ##dm=σ*a*dx##, and ##m=σ*L*H##, where ##σ=ρ*D##. also, let K be the kinetic energy and U dynamic potential energy. then, ##K={1 \over 2 }*m*u^2##, ##U=mg(y-y_o)##. because ##{dE \over dt}=0## (we assumed we have simple harmonic oscillations) and ##E=K+U##, we find that ##(y-y_o)~u^2##. the main problem here is what assumptions would i be correct to make about the relationship of ##(x-x_o)## and velocity u? how would i compute frequency?
thank you for reading.
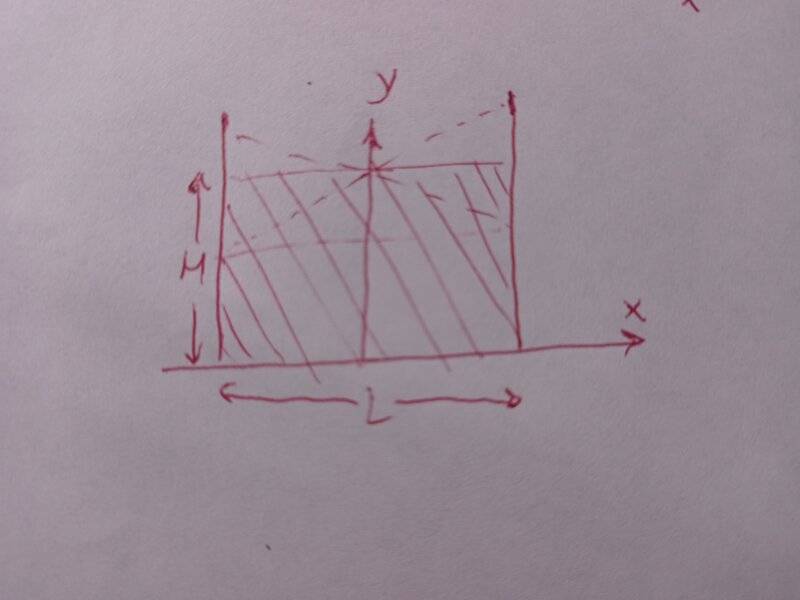
in container with dimensions L×D, rests water of height H and density ρ. we disturb the water along L dimension, and accept an oscillation is caused on the free surface of the water, which maintains its flatness, so that the central of mass of the water moves up-down and left-right, and the water does not move in the extreme positions but only has change in potential energy due to gravity, while in the middle positions where the surface is horizontal, all the energy gets converted to kinetic energy. say the central of mass is in position ##(x_o,y_o)## in equilibrium, and ##(x,y)## during the oscillation. how do we show that ##mg(y-y_o)## is proportional to ##(x-x_o)^2##, and find cyclic frequency of the oscillation of the water?
i have tried to prove said proportionality using conservation of energy as follows: for every column of height ##(H+a)##, it is ##dm=σ*a*dx##, and ##m=σ*L*H##, where ##σ=ρ*D##. also, let K be the kinetic energy and U dynamic potential energy. then, ##K={1 \over 2 }*m*u^2##, ##U=mg(y-y_o)##. because ##{dE \over dt}=0## (we assumed we have simple harmonic oscillations) and ##E=K+U##, we find that ##(y-y_o)~u^2##. the main problem here is what assumptions would i be correct to make about the relationship of ##(x-x_o)## and velocity u? how would i compute frequency?
thank you for reading.
Last edited: