Output as the convolution of the Impulse response and input

[cnh1995]

As the title says, I am studying this topic for my control systems fundamentals course. I think I intuitively understand the meaning of the convolution integral that relates input, output and the impulse response, but I am failing to prove it graphically.
For example, the intuitive explanation for this convolution integral is as follows:
Any input can be represented by using time shifted and weighted impulses in succession, and the output at any time t is the superposition of individual impulse responses obtained from each impulse.
This makes sense, but when I try plot it on paper, something looks wrong.

For input x(t)=1...(x>=0) and impulse response h(t)=e^-t, output y(t)= 1-e^-t

Input:

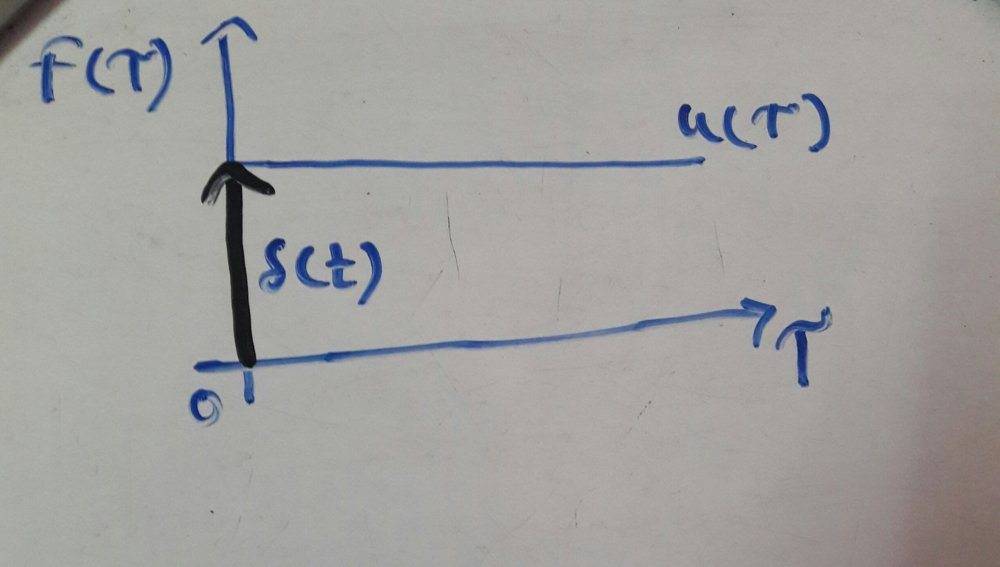
Impulse reaponse:

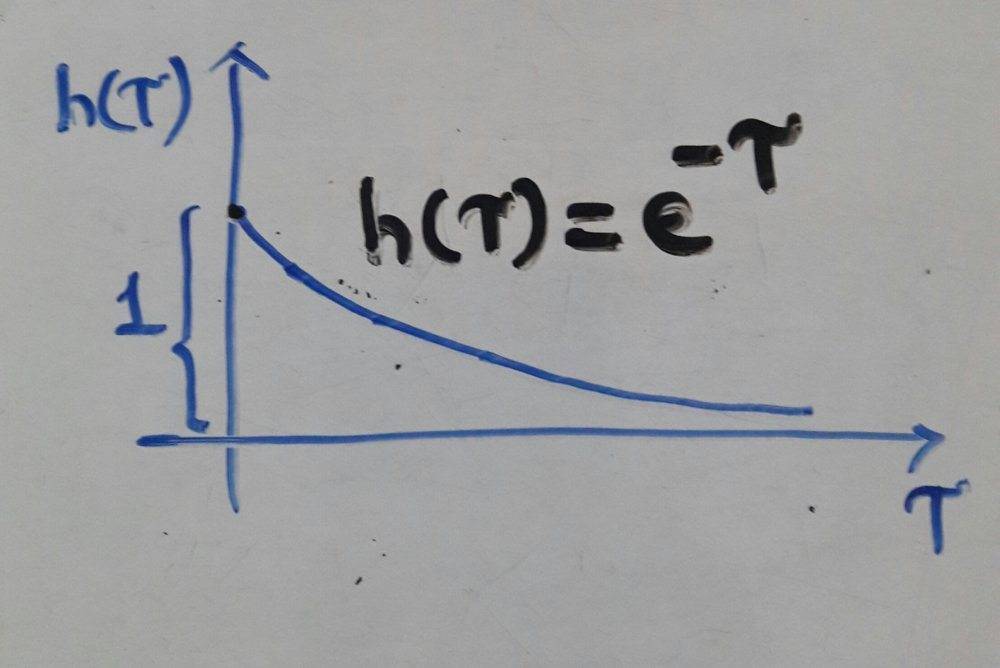
Output:

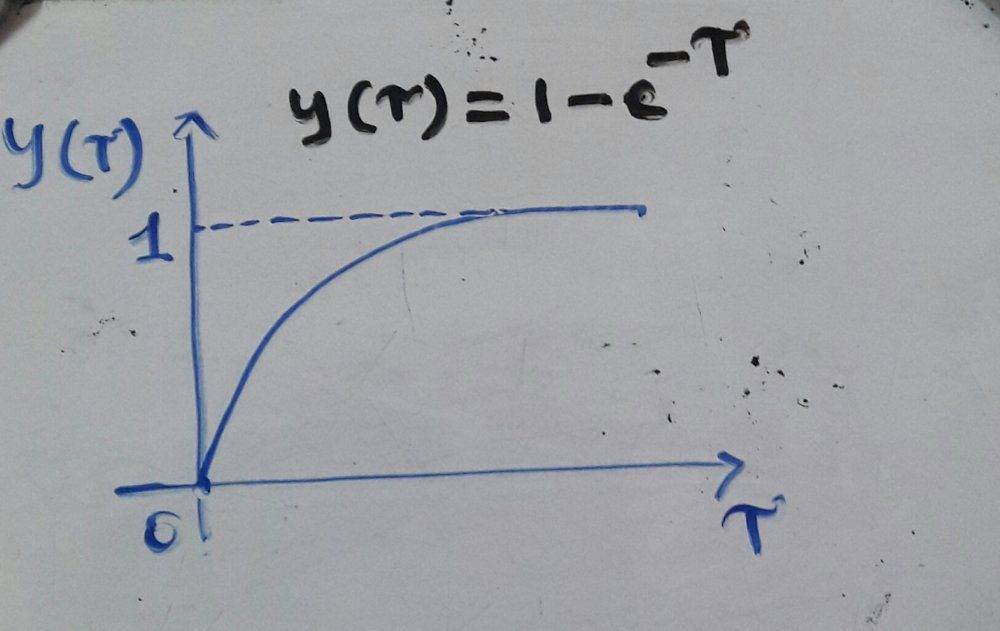
Here, output y(0)=0, but impulse response h(0)=1. What makes y(0)=0 then?
Also, if I pick any instant t=a, the superposition of all the exponentially decaying impulse reaponses at t=a does not seem to give me the correct value of y(a). Where is my mistake? I feel I am missing something very fundamental here.

Thanks!

 

[wirefree]

Thanks for asking this question. It’s a topic I hoped to revise myself. Maybe I can guide you along a lil’ further.

You’ve already done the hard word of describing your concerns in detail, so I’ll just pick up from there.

Any input can be represented by using time shifted and weighted impulses in succession, and the output at any time t is the superposition of individual impulse responses obtained from each impulse.

I sense a slight discrepancy there.

With regards to the input, the definition you provide is correct, but it’s not translating to the input graphic below in that I would have drawn an impulse train, as opposed to the single impulse at zero, to comply with the “weighted & shifted” section of the definition.

With respect to the output definition, again a slight error, but one I suspect might lie at the root of your concern: “the output at any time t is the superposition of individual impulse responses obtained from each impulse” if the input was a unit impulse, which in the case you are considering is not; your input is a unit step function, i.e. x(t)=1 for t>0.

Output:
View attachment 246013

Here, output y(0)=0, but impulse response h(0)=1. What makes y(0)=0 then?

I suspect that here you would just be required to meditate a little more on the idea of superposition, because when you grasp it you’d realize the mistake of ascribing a value to the output at a point based just on the value of the impulse response at that point, since, to obtain a value of the output at a given point, you would shift your impulse response from -ve to +ve infinity, multiply it with the input at every point, and add the all the results at the point of interest to obtain the output value.So, in all, not much here; just a couple of things mostly centered on superposition. But I am happy to continue this conversation.wirefree

 

[AVBs2Systems]

Hi chnI believe the answer can be found by thinking about the definition of convolution, also are you using the correct definition of the unit step function?
$$

\text{The unit step function} \,\,\,\,\,\, \epsilon(t) = \begin{cases} 1 & \text{if $ t $ } \gt 0 \\ 0 & \text{Otherwise} \end{cases}
$$

$$
y(t) = x(t) * h(t) = \displaystyle \int_{-\infty}^{\infty} x(\tau) \cdot h(t - \tau ) \,\,\,\, \text{d}\tau
$$So at the point where $$
x(\tau=0) = 0
$$
and
$$
h(t - \tau = 0) = 1$$
we get

$$
y(0) = x(0) * h(0) = \displaystyle \int_{-\infty}^{\infty} \bigg( x(0) = 0 \bigg) \cdot \bigg( h(0) = 1 \bigg) \,\,\,\, \text{d}\tau = 0
$$

 

[rude man]

See attached pdf file of a scan from Principles of the Statistical Theory of Communication by Stanford Prof. W W Harman, McGraw-Hill. An excellent text BTW, highly recommended.

(By now I assume that Stanford professors are not be taken lightly! )

 

[DaveE]

See attached pdf file of a scan from Principles of the Statistical Theory of Communication by Stanford Prof. W W Harman, McGraw-Hill. An excellent text BTW, highly recommended.

(By now I assume that Stanford professors are not be taken lightly! )

You can tell it's a communications text because he uses Fourier transforms. Controls types would use Laplace, LOL. They are both correct of course.

 

[rude man]

Statistical control system design requires addressing negative as well as positive time. What most people refer to as the "Laplace Transform" is in reality the One-Sided Laplace transform.

Samuel Seely's Control System Synthesis does indeed use the uses the two-sided Laplace, giving as reason the wide familiarity with the single-sided Laplace & expanding from it. I believe however that nearly every other author uses the Fourier. I have dealt with both, am IMO pretty familiar with the one-sided Laplace, but have to go with the majority in this case.Maybe it's because the Fourier inversion integral is one-dimensional whereas the Laplace is of course two, and the Fourier can do what the one-sided Laplace can't, so it seems more versatile. I believe physicists are pretty much Fourier types wheras EE's of course love that good old "Laplace".

BTW I have also found that doing convolution graphically in the time domain is usually way simpler than going to transforms, at least with deterministic problems.