Oven controller block diagram, transfer function and temperature calcs

Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
Sign up Log in
24 replies · 6K views
Anfo
Messages
9
Reaction score
0
Homework Statement
Anyone able to help a bit? I have drawn the block diagram but don't think it's quite right.
Relevant Equations
.
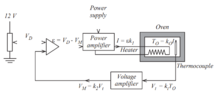
FIGURE 5 shows an electrically heated oven and its associated control
circuitry. The current, I, to the oven's heating element is fed from a
voltage-controlled power amplifier such that I = EK1. A voltage, VD, derived
from a potentiometer, sets the desired oven temperature, TD. The oven
temperature is measured using a thermocouple that, for simplicity, is
assumed to generate a constant emf of 10 uV per degree Celsius. The effect
of the ambient temperature is ignored.
1681579496946.png
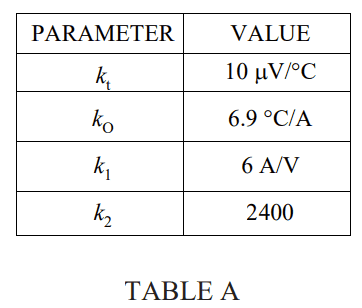
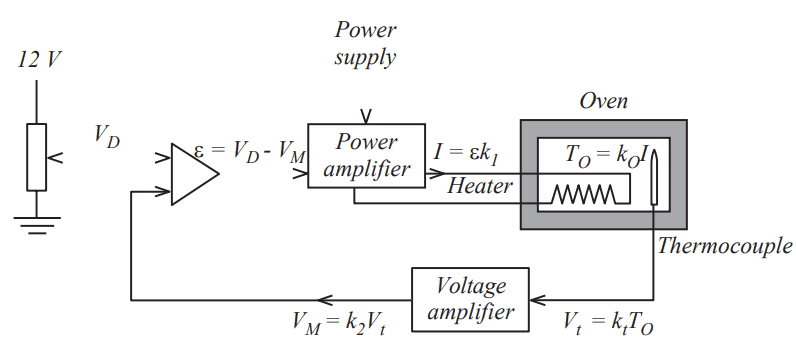(a) Represent the arrangement by a conventional control-system block diagram. Identify the following elements in the block diagram: input; error detector (comparator); controller; controlled element; detecting element and feedback loop. (b) Derive an expression for the transfer function of the system, in terms of the system parameters k1, k2, kO and kt. (c) Using the data given in TABLE A, calculate the oven temperature when the potentiometer is at its mid-point.

1681579547230.png
 

Attachments

  • 1681579399390.png
    1681579399390.png
    11.1 KB · Views: 217
Physics news on Phys.org
Also, I'm a bit confused as to where K2 will be. The power amp is K1 and the oven is Ko?
 
Anfo said:
Homework Statement: Anyone able to help a bit? I have drawn the block diagram but don't think it's quite right.
Can you upload your attempt at a solution?
 
Mark44 said:
I believe the block diagram in post #1 is the attempt so far.
Anfo said:
FIGURE 5 shows an electrically heated oven and its associated control
circuitry.
I think the diagram is provided along with the problem statement and the OP is asked to develop its control-system block diagram from this.
 
I am new to this subject and a bit confused as to where the output will sit. Is that Ko?
 
Needless to say I need to get this part right to be able to work out the transfer function expression. Apologies if a stupid question but any help or guidance will be much appreciated!
 
Anfo said:
I am new to this subject and a bit confused as to where the output will sit. Is that Ko?
I only see a lower case ##k_0## in this exercise, and it is a fixed parameter (6.9 ##^\circ C/A##).
I would expect the oven temperature is a good candidate for the quantity that is to be controlled.

In your picture:
  • The heating element converts a current into a temperature. There is no ##k_t## there (and no ##K_t## either)
  • I miss
    • In the feedback path: the thermocouple
Next step: write out the transfer function

##\ ##
 
Reply
  • Like
Likes   Reactions: cnh1995 and berkeman
I see what you mean, so I would need to add another block in the feedback path for the thermocouple. The small signal will then be amplified by the voltage amplifier.

I have started to put the transfer function together but am a bit unsure.

E = Vd - Vm
but Vm = k2 x Vt
so E = Vd - (k2 * Vt)
but Vt = kt * To
so E = Vd -(k2 * kt * To)

We know the potentiometer is at midpoint so Vd = 6V

Plugging known values into the above equation I get the oven temp To = 208.33degC?

Does that sound right?
 
From this:

E = Vd - Vm
but Vm = k2 x Vt
so E = Vd - (k2 * Vt)
but Vt = kt * To
so E = Vd -(k2 * kt * To)

I have substituted further to:
To = ko * I
so E = Vd - (k2 * kt * ko * I)
and I = E * k1
so final transfer function is E = Vd - (k2 * kt * ko * E * k1)

I have worked out E to be = 1 and I = 6A
Plugging in all the known values gives an answer of To = 208.33degC

I am not sure if this is right and was purely messing around with substituting into E = Vd - Vm.

I'd appreciate any comments!
 
Anfo said:
so final transfer function is E = Vd - (k2 * kt * ko * E * k1)
You have E on the righthand side AND on the lefthand side. More work is needed !

I would expect the transfer function to express ##T_0## as a function of ##V_D## !

[edit] Furthermore: 6 A times ##k_0## is 41 degrees, not 208 !!!

##\ ##
 
This is the bit where I got stuck. E is again on the right because To = ko * I and I = E * k1

Maybe I'm taking the substitution level too far?
 
No, not far enough ! It's important, so I will spell it out: Write ##T_0## as a function of ##V_D##. If it contains a term with ##V_M## (and it does...), write that as a function of ##T_0## . Then bring all terms with ##T_0## to the left.

Standard procedure with feedback loops. :smile:

[edit]

And with operational amplifiers too. Very useful, so let me explain (from control engineering 101, 50 years ago :wink: ) :

1681899475422.png


Under condition of linearity: going straight from x to y:$$\begin {align*} y &= F(x-z) = F(x)-F(z) \\ \ \\ z & = G(y) \\ \ \\
y&=F(x) - FG(y) \\ \ \\ (1+FG)\;y &= F(x) \\ \ \\ y &= {F\over 1+FG}\ x \end {align*}$$

##{F\over 1+FG} ## is the transfer function. As you can see, trouble breaks out when ##FG=-1## ...

##\ ##
 
Last edited:
Reply
  • Like
Likes   Reactions: berkeman
It makes total sense now! Actually so simple really but if you don't know then you don't know.
Brilliant, thanks so much. I will play with this now and see what results I get for the oven temperature.
 
Anfo said:
been a bit busy with work and not much time to get back to studying.

Calculated the oven temperature to 124 degC. Do you think this is right?
It's your result, so you 'll have to convince yourself that it's correct !

Personally, I liked the expression ##\displaystyle{T=V_D\,{ k_1 k_0\over 1+k_1 k_0 k_t k_2}}## much better than the numerical outcome: You can check the dimensions (to check the line of thought) and estimate the order of magnitude of the result (to check the calculator work).

But if I would have found something different, this post wouldn't have been as it is now :smile:

[edit] although there is the small matter of properly rounding off ...

##\ ##
 
Last edited:
Question: Was the function as given above derived from the block diagram in post#8 ?
If yes - it is wrong!
 
Anybody know how to Derive an expression for the transfer function of this question?? I have seen the answers above but still dont understand. Any ideas??
 
#17 and #19 should give you a clue!
If they don't: why not?

Grafter said:
Anybody know how to Derive an expression for the transfer function of this question?? I have seen the answers above but still dont understand. Any ideas??
Hard to help if we don't know where or why you get stuck.
What is your approach/reasoning ?

##\ ##
 
Reply
  • Like
Likes   Reactions: berkeman
Sorry I am not electronically biased... I have the following, E = Vd-Vm, I = Ek1, To = k0I, Vt= ktTo, Vm = k2Vt
Any help would be greatly appreciated
 
Grafter said:
I have the following
Copying the problem statement wasn't what I had in mind ...

Grafter said:
I am not electronically biased...
No need to apologize for that :wink:. But the exercise really is aimed at a pretty broad audience (like those who cook a goose or a turkey at some point in their life).

Seriously: what about the hints in #11 and #15 ?

[edit] And I pointed out #17 and #19 to you; what did you pick up from those ?

##\ ##