hicetnunc
- 13
- 5
- Homework Statement
- Show that the overlap integral of a 1s orbital and a 2p orbital from hydrogen forming a ##\sigma## bond is
$$S = \frac{R}{a_0} \Big[ 1 + \frac{R}{a_0} + \frac{1}{3} \Big( \frac{R}{a_0} \Big)^2 \Big] e^{-R/a_0}$$
where ##R## is the distance between the atoms.
- Relevant Equations
- None.
Hi! Some help with this problem would be much appreciated.
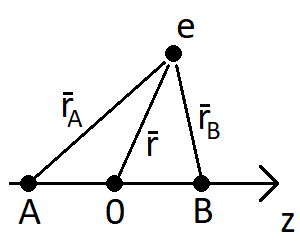
The overlap integral is defined as ##S = \int \phi_A (\mathbf{r}_A) \phi_B (\mathbf{r}_B) \,d\mathbf{r}##. For the two orbitals, I have that
$$\phi_A = \frac{1}{\sqrt{\pi}} \Big( \frac{1}{a_0} \Big)^{3/2} e^{-r_A / a_0}$$
for the 1s orbital and
$$\phi_B = \frac{1}{4\sqrt{2\pi}} \Big( \frac{1}{a_0} \Big)^{5/2} \cos \theta r_B e^{-r_B / 2a_0} $$
for the 2p orbital. This would give an overlap integral of
$$S = \frac{1}{4\sqrt{2}\pi} \Big( \frac{1}{a_0} \Big)^4 \int \cos \theta r_B e^{-(r_A+0.5r_B)/a_0} \,d\mathbf{r}$$
Now, the textbook I'm using suggests using spheroidal coordinates ##u=\frac{r_A + r_B}{R}## and ##v=\frac{r_A - r_B}{R}##. Since ##\theta## is the angle between ##r_B## and the z-axis, this gives me ##\cos \theta = \frac{z - R/2}{r_B}## and since ##z=\frac{R}{2}uv## I get ##\cos \theta = \frac{R(uv-1)}{2 r_B}##. The overlap integral is now
$$S = \frac{R}{8\sqrt{2}\pi a_0^4} \int (uv-1) e^{-R(3u-v)/(4a_0)} \,d\mathbf{r}$$
The volume element is ##\frac{R^3}{8}(u^2-v^2)## and the variables ##(u, v, \theta')## have the intervals ##1 \leq u \leq \infty##, ##-1 \leq v \leq 1## and ##0 \leq \theta' \leq 2\pi##.
But I can't get the same solution for this integral as stated in the exercise. Already from the beginning I have a factor of ##1 / \sqrt{2}## that will follow through and not disappear. I've tried solving the integral, but it's a really tedious and long calculation. Do I at least have the right integral?
I've done a similar version of this exercise for a hydrogen molecule with two 1s orbitals, and got the right solution for that. That integral was MUCH easier to solve than this.
The overlap integral is defined as ##S = \int \phi_A (\mathbf{r}_A) \phi_B (\mathbf{r}_B) \,d\mathbf{r}##. For the two orbitals, I have that
$$\phi_A = \frac{1}{\sqrt{\pi}} \Big( \frac{1}{a_0} \Big)^{3/2} e^{-r_A / a_0}$$
for the 1s orbital and
$$\phi_B = \frac{1}{4\sqrt{2\pi}} \Big( \frac{1}{a_0} \Big)^{5/2} \cos \theta r_B e^{-r_B / 2a_0} $$
for the 2p orbital. This would give an overlap integral of
$$S = \frac{1}{4\sqrt{2}\pi} \Big( \frac{1}{a_0} \Big)^4 \int \cos \theta r_B e^{-(r_A+0.5r_B)/a_0} \,d\mathbf{r}$$
Now, the textbook I'm using suggests using spheroidal coordinates ##u=\frac{r_A + r_B}{R}## and ##v=\frac{r_A - r_B}{R}##. Since ##\theta## is the angle between ##r_B## and the z-axis, this gives me ##\cos \theta = \frac{z - R/2}{r_B}## and since ##z=\frac{R}{2}uv## I get ##\cos \theta = \frac{R(uv-1)}{2 r_B}##. The overlap integral is now
$$S = \frac{R}{8\sqrt{2}\pi a_0^4} \int (uv-1) e^{-R(3u-v)/(4a_0)} \,d\mathbf{r}$$
The volume element is ##\frac{R^3}{8}(u^2-v^2)## and the variables ##(u, v, \theta')## have the intervals ##1 \leq u \leq \infty##, ##-1 \leq v \leq 1## and ##0 \leq \theta' \leq 2\pi##.
But I can't get the same solution for this integral as stated in the exercise. Already from the beginning I have a factor of ##1 / \sqrt{2}## that will follow through and not disappear. I've tried solving the integral, but it's a really tedious and long calculation. Do I at least have the right integral?
I've done a similar version of this exercise for a hydrogen molecule with two 1s orbitals, and got the right solution for that. That integral was MUCH easier to solve than this.