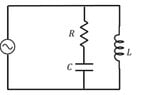
- #1
lys04
- 95
- 4
- Homework Statement
- How can I graph the impedance against the frequency using a logarithmic scale for the frequency axis?
- Relevant Equations
- $$ Z = \frac{iwL-w^{2}RLC}{1-w^{2}LC+iwRC} $$
^^ as mentioned in the homework statement, the relevant equation is my worked out impedance for the circuit. I have attached a diagram of the circuit below.