Parameters in Bohr-Mottelson Collective Hamiltonian

[patric44]

Homework Statement:

how do I find the value of the mass parameter and the width of the potential well present in the Bohr-Mottelson Hamiltonian?

Relevant Equations:

-hbar^2/2B

Hi all
I was reading a certain paper that involves solving the Bohr-Mottelson Hamiltonian for a 5dimential square well potential, the B-M Hamiltoian reads:

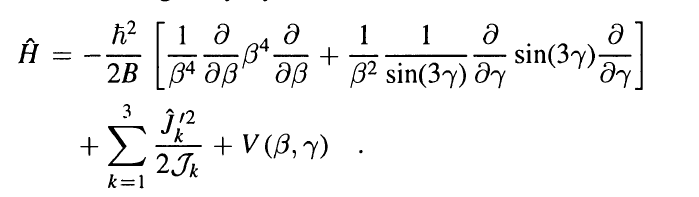
my question is just how do I calculate the mass parameter "B" for a certain nuclei, and with a 5D infinite potential well how do I get the width of the potential well?
I will appreciate any help, thanks in advance.

 

[patric44]

can any one suggest a paper or a book that address these points