mathlearn
- 331
- 0
Part 1 : http://mathhelpboards.com/pre-algebra-algebra-2/draw-venn-diagram-include-given-information-19723.html#post90092
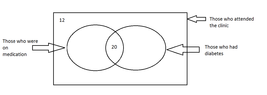
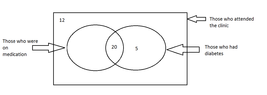
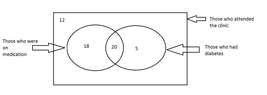
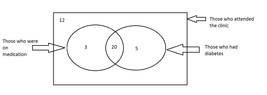
Among the 40 persons who visited the clinic , there were persons who were on medication and those who were not on medication as well. An incomplete Venn diagram drawn using this information is shown below
https://www.physicsforums.com/attachments/6060._xfImport
iii . Copy the Venn diagram given above and write down the values relevant to the two empty regions in it.
iv. How many persons had diabetes but were not on medication.
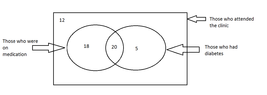
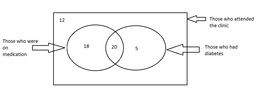
Among the 40 persons who visited the clinic , there were persons who were on medication and those who were not on medication as well. An incomplete Venn diagram drawn using this information is shown below
https://www.physicsforums.com/attachments/6060._xfImport
iii . Copy the Venn diagram given above and write down the values relevant to the two empty regions in it.
iv. How many persons had diabetes but were not on medication.
Attachments
Last edited: