Kris1
- 29
- 0
Partial Derivatives
Hi all I was wondering if anyone could help me with this problem. I have a triangle that has a = 13.5m, b = 24.6m c, and theta = 105.6 degrees.
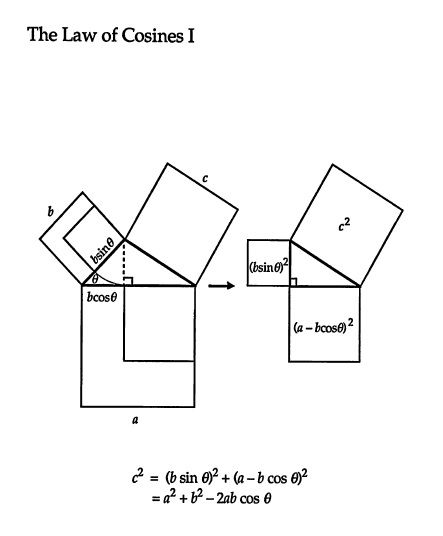
Can someone remind me of what the cosine rule is?
Also (my question is here)
From the cosine rule i need to find:
How would i go about finding these partial derivatives for these? Do I need to know what the cosine rule is and what the value of c is?
How to find the partial derivatives?
Any help will be appreciated.
Hi all I was wondering if anyone could help me with this problem. I have a triangle that has a = 13.5m, b = 24.6m c, and theta = 105.6 degrees.
Can someone remind me of what the cosine rule is?
Also (my question is here)
From the cosine rule i need to find:
- the partial derivative of c with respect to a?
- the partial derivative of c with respect to b?
- the partial derivative of c with respect to theta?
How would i go about finding these partial derivatives for these? Do I need to know what the cosine rule is and what the value of c is?
How to find the partial derivatives?
Any help will be appreciated.
Last edited by a moderator: