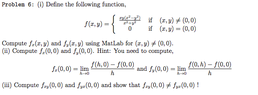Partial Derivatives Problem Evaluating at (0,0)

[Jamie2]

Problem: View attachment 2084I did some of the problem on MatLab but I'm having a difficult time evaluating the derivatives at (0,0). Also, MatLab gave me the same answer for f_xy and f_yx, which according to the problem isn't correct. Any ideas? I used MatLab and computed:

f_x(x,y)=(2*x^2*y)/(x^2 + y^2) + (y*(x^2 - y^2))/(x^2 + y^2) - (2*x^2*y*(x^2 - y^2))/(x^2 + y^2)^2

and

f_y(x,y)=(x*(x^2 - y^2))/(x^2 + y^2) - (2*x*y^2)/(x^2 + y^2) - (2*x*y^2*(x^2 - y^2))/(x^2 + y^2)^2

I also used MatLab to compute f_xy and f_yx, both gave me the same answer:

(x^2 - y^2)/(x^2 + y^2) + (2*x^2)/(x^2 + y^2) - (2*y^2)/(x^2 + y^2) - (2*x^2*(x^2 - y^2))/(x^2 + y^2)^2 - (2*y^2*(x^2 - y^2))/(x^2 + y^2)^2 + (8*x^2*y^2*(x^2 - y^2))/(x^2 + y^2)^3

 

[Opalg]

The Matlab answers for $f_{xy}$ and $f_{yx}$ are valid when $(x,y)\ne(0,0)$. The only point at which $f_{xy} \ne f_{yx}$ is when $(x,y) = (0,0).$ So you need to calculate $f_{xy}(0,0)$ and $f_{yx}(0,0).$ You need to do this from first principles, using the definition of the derivative as a limit.

You first need to check that $$f_x(0,0) = \lim_{h\to0}\frac{f(h,0) - f(0,0)}h = \lim_{h\to0}\frac{\frac {h*0(h^2-0^2)}{h^2+0^2} - 0}h = 0.$$ The next step is to calculate $$f_{xy}(0,0) = \frac{\partial f_x}{\partial y}(0,0) = \lim_{k\to0}\frac{f_x(0,k) - f_x(0,0)}k$$ in a similar way. Then do the same for $f_y(0,0)$ and $f_{yx}(0,0)$.

 

[Jamie2]

The Matlab answers for $f_{xy}$ and $f_{yx}$ are valid when $(x,y)\ne(0,0)$. The only point at which $f_{xy} \ne f_{yx}$ is when $(x,y) = (0,0).$ So you need to calculate $f_{xy}(0,0)$ and $f_{yx}(0,0).$ You need to do this from first principles, using the definition of the derivative as a limit.

You first need to check that $$f_x(0,0) = \lim_{h\to0}\frac{f(h,0) - f(0,0)}h = \lim_{h\to0}\frac{\frac {h*0(h^2-0^2)}{h^2+0^2} - f(0,0)}h = 0.$$ The next step is to calculate $$f_{xy}(0,0) = \frac{\partial f_x}{\partial y}(0,0) = \lim_{h\to0}\frac{f_x(0,k) - f_x(0,0)}k$$ in a similar way. Then do the same for $f_y(0,0)$ and $f_{yx}(0,0)$.

the problem is that when I try to use the limit definition of the derivative I get that it's undefined (0/0). Do you have any suggestions for how I can compute that limit?

 

[Opalg]

the problem is that when I try to use the limit definition of the derivative I get that it's undefined (0/0). Do you have any suggestions for how I can compute that limit?

The result I get by using the quotient rule (which I hope agrees with the Matlab result except that I have tried to simplify it a bit) is $$f_x(x,y) = \frac{\bigl(y(x^2-y^2) + 2x^2y\bigr)(x^2+y^2) - 2x^2y(x^2-y^2)}{(x^2+y^2)^2} = \frac{y(x^4-y^4) + 4x^2y^3}{(x^2+y^2)^2}.$$ Then when you put $x=0$ and $y=k$ you get $$f_x(0,k) = \frac{-k^5}{k^4} = -k.$$ Now put that into the expression for $f_{xy}(0,0)$ and you get $$f_{xy}(0,0) = \lim_{k\to0}\frac{f_x(0,k) - f_x(0,0)}k = \lim_{k\to0}\frac{-k - 0}k = -1.$$ My guess is that when you do the same thing for $f_{yx}(0,0)$, the answer will come out as $+1.$

 

[Jamie2]

The result I get by using the quotient rule (which I hope agrees with the Matlab result except that I have tried to simplify it a bit) is $$f_x(x,y) = \frac{\bigl(y(x^2-y^2) + 2x^2y\bigr)(x^2+y^2) - 2x^2y(x^2-y^2)}{(x^2+y^2)^2} = \frac{y(x^4-y^4) + 4x^2y^3}{(x^2+y^2)^2}.$$ Then when you put $x=0$ and $y=k$ you get $$f_x(0,k) = \frac{-k^5}{k^4} = -k.$$ Now put that into the expression for $f_{xy}(0,0)$ and you get $$f_{xy}(0,0) = \lim_{k\to0}\frac{f_x(0,k) - f_x(0,0)}k = \lim_{k\to0}\frac{-k - 0}k = -1.$$ My guess is that when you do the same thing for $f_{yx}(0,0)$, the answer will come out as $+1.$

I am not sure that this is what the question is asking. Basically I just need help solving the limit definition of derivative algebraically because every time I try I get 0/0= undefined.
I need to show the value of the derivative for f(x,y)= xy(x^2-y^2)/(x^2+y^2), at fx(0,0) and at fy(0,0) using the limit definition of derivative for both.

 

[Opalg]

I am not sure that this is what the question is asking. Basically I just need help solving the limit definition of derivative algebraically because every time I try I get 0/0= undefined.
I need to show the value of the derivative for f(x,y)= xy(x^2-y^2)/(x^2+y^2), at fx(0,0) and at fy(0,0) using the limit definition of derivative for both.

If you look at part (iii) of the question, you will see that that is exactly what I have indicated how to do. (Nod)