Particle dynamics (mechanics): inclined plane, pulley, two blocks

[Memo]

Homework Statement

(the photo is below) The angle between the inclined plane and the surface is α. The coefficient of friction between block 2 and the inclined plane is k. Find the ratio inequality of m1 over m2 that the system remains still.

Answer: for m2 to go down: m1/m2>sina+k∗cosa

for m2 to go up: m1/m2<sina−k.cosa

For the system to remain balanced: sina−k.cosa<m1/m2<sina+k.cosa

Could somebody explain to me why the answer should be the above and not sina+k.cosa<m1/m2<sina−k.cosa?
Thank you very much!!!

Relevant Equations

I combined the two inequalities but it doesn't match the answer hints so I'd love it if someone could explain to me how that makes sense.

(sorry for my poor English)

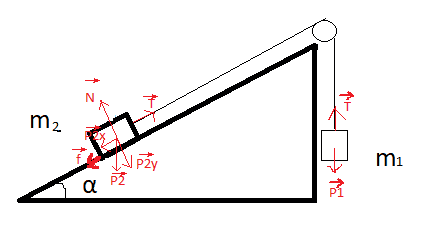
+For m1 to go down, the Net force acting on m1 must be smaller than 0 -> T-m1*g<0 -> T<m1*g(1)
_Evaluating object 2 perpendicularly: N-Py2=0 -> N=m2*g*cosa
_Evaluating object 2 parallel: -Px-f+T=0 -> T=sina*g*m2 + k*m2*g*cosa (2)
_Insert 2 into 1: m1g > sina*g*m2 + k*m2*g*cosa -> m1 > m2*(sina+kcosa) -> m1/m2 > sina + kcosa

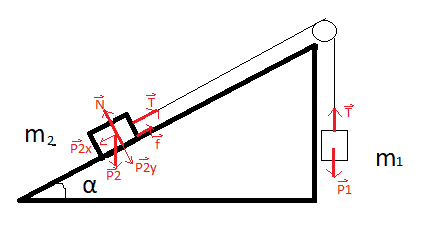
+For m1 to go up, the Net force acting on m1 must be greater than 0 -> T-m1*g>0 -> T>m1*g (3)
_Evaluating object 2 parallel: -Px+f+T=0 -> T=sina*g*m2 - k*m2*g*cosa (4)
_Insert 4 into 3: m1/m2 < sina - k*cosa

+For the system to remain still, the tension force must be within the range when the objects are on the verge of moving.
(so I combine the two inequalities and get sina + k*cosa < m1/m2 < sina - k*cosa but the answer hints isn't the same)

 

[kuruman]

First of all the diagram does not match the statement of the problem. The diagram shows block $m_1$ on the incline but the problem says "The coefficient of friction between block 2 and the inclined plane is k." We will go by the diagram.

Secondly, you need to draw two free body diagrams (FBDs)
FBD_1 for the block on the incline when it is just about to slide up but is still at rest.
FBD_2 for the block on the incline when it is just about to slide down but is still at rest.

That should show you how the forces on the block add. Also note that the tension in this case is equal to the weight of the hanging block. Write out the forces first, then consider taking the ratio of masses.

 

[Memo]

First of all the diagram does not match the statement of the problem. The diagram shows block $m_1$ on the incline but the problem says "The coefficient of friction between block 2 and the inclined plane is k." We will go by the diagram.

Secondly, you need to draw two free body diagrams (FBDs)
FBD_1 for the block on the incline when it is just about to slide up but is still at rest.
FBD_2 for the block on the incline when it is just about to slide down but is still at rest.

That should show you how the forces on the block add. Also note that the tension in this case is equal to the weight of the hanging block. Write out the forces first, then consider taking the ratio of masses.

First of all, I'm so sorry for the wrong image I put there. Secondly, I did draw the FBD for the two objects in both cases (m1 go up and down) to conclude the 2 inequalities above (which matchs the answer hints). And finally, the task requires me to find the inequality ratio, so that's why I can't put T=m1*g. Thank you very much for replying, but could you help me further

 

[kuruman]

Secondly, I did draw the FBD for the two objects in both cases (m1 go up and down) to conclude the 2 inequalities above (which matchs the answer hints).

Where are they? I don't see them anywhere.

And finally, the task requires me to find the inequality ratio, so that's why I can't put T=m1*g.

Whatever the task requires you to do, when the hanging mass is not accelerating, the tension is $T=m_1g.$ There are only two forces acting on $m_1$, the tension and gravity. If they are not equal, it will be accelerating. Remember, the FBDs are drawn when the two masses are just about to start sliding but they are still at rest. Only then you can you set the force of friction equal to the normal force times the coefficient of friction $k$.

Thank you very much for replying, but could you help me further

Not right now. It's late where I am and I need some sleep. I am sure someone else will be happy to help you.

 

[Memo]

Where are they? I don't see them anywhere.

Whatever the task requires you to do, when the hanging mass is not accelerating, the tension is $T=m_1g.$ There are only two forces acting on $m_1$, the tension and gravity. If they are not equal, it will be accelerating. Remember, the FBDs are drawn when the two masses are just about to start sliding but they are still at rest. Only then you can you set the force of friction equal to the normal force times the coefficient of friction $k$.

Not right now. It's late where I am and I need some sleep. I am sure someone else will be happy to help you.

I'm new to this site so I didn't put the diagrams here, but I did draw them on my draft and use them to solve for case 1 (when m1 goes up) and 2 (m1 goes down).
Thank you very much for pointing this out, but I think the task is challenging learners

 

[haruspex]

I'm new to this site so I didn't put the diagrams here, but I did draw them on my draft and use them to solve for case 1 (when m1 goes up) and 2 (m1 goes down).
Thank you very much for pointing this out, but I think the task is challenging learners

Your attachment link no longer works. Please load the diagram directly into a post.

 

[Memo]

Your attachment link no longer works. Please load the diagram directly into a post.

 

[erobz]

Could somebody explain to me why the answer should be the above and not sina+k.cosa<m1/m2<sina−k.cosa?
Thank you very much!!!

For starters $\alpha$ is in the first quadrant which implies $\sin \alpha > 0, \cos \alpha > 0$, and (I think) we have that $k>0$.

Logically, can there exist a number that is larger than $\sin \alpha + k \cos \alpha$, while also being less than $\sin \alpha - k \cos \alpha$ like you are implying exists with that inequality?

 

[Steve4Physics]

For the system to remain balanced: sina−k.cosa<m1/m2<sina+k.cosa

Could somebody explain to me why the answer should be the above and not sina+k.cosa<m1/m2<sina−k.cosa?

Your working is difficult to follow but you seem to have a sign convention (+/-) error and/or an error with the direction of friction.

The frictional forces shown on your diagrams don’t match your text. E.g. when $m_2$ is about to start sliding downhill, the frictional force on it is uphill (but your diagram shows it downhill).

 

[erobz]

It's best if you clearly state your conventions in each diagram by putting directional arrows and a $+$ sign, so we are not required to re-engineer them to check consistency. For example:

 

[kuruman]

The frictional forces shown on your diagrams don’t match your text. E.g. when m2 is about to start sliding downhill, the frictional force on it is uphill (but your diagram shows it downhill).

Yes, the diagrams are reversed because I suspect @Memo does not understand what they depict.

To @Memo:
Both that you have posted presumable show the blocks at rest. This means that the acceleration is zero. Suppose you have zero hanging mass and $m_2$ is at rest on the incline. Then you have force $P_{2x}=-m_2~g~\sin\!\alpha$ which means that $f$ and points up the incline and the net force is zero: $-m_2~g~\sin\!\alpha+f=0\implies f=m_2~g~\sin\!\alpha.$

Now suppose you attach small hanging mass $m_1$ to $m_2$ and $m_2$ still doesn't accelerate. First of all the tension T is $m_1g$ because if $m_1$ doesn't accelerate, $m_2$ also doesn't accelerate. So what do we have?
Down the incline we still have $P_{2x}=-m_2~g~\sin\!\alpha.$
Up the incline we have $f'+T=f'+m_1g.$
For equilibrium $-m_2~g~\sin\!\alpha+f'+m_1g=0 \implies f'=m_2~g~\sin\!\alpha-m_1g$
You see that the friction $f'$ needed to maintain the equilibrium has a smaller value than when no mass was hanging. Its magnitude was reduced by and amount equal to the hanging weight.

So you see, as you hang more and more weight $m_1$ the friction will get smaller until in becomes zero. At that point no friction is needed to maintain equilibrium. If you increase $m_1$ past that point, friction $f$ will start pointing down the incline and it will grow in magnitude as you increase $m_1$. Can the friction grow forever? No and at some point (what point?) $m_2$ will start sliding uphill.

So I will ask you again what is the direction of the force of friction when $m_1$ starts sliding uphill?

 

[Memo]

For starters $\alpha$ is in the first quadrant which implies $\sin \alpha > 0, \cos \alpha > 0$, and (I think) we have that $k>0$.

Logically, can there exist a number that is larger than $\sin \alpha + k \cos \alpha$, while also being less than $\sin \alpha - k \cos \alpha$ like you are implying exists with that inequality?

I understand now, thank you so much!

 

[Memo]

Your working is difficult to follow but you seem to have a sign convention (+/-) error and/or an error with the direction of friction.

The frictional forces shown on your diagrams don’t match your text. E.g. when $m_2$ is about to start sliding downhill, the frictional force on it is uphill (but your diagram shows it downhill).

Normally I draw the diagram first and then solve the task, but I'm new to this site so I don't know how to fix it. In this case, you can observe it as I solved the math and then I drew the diagram. I believe you're looking at diagram 1 (m1 goes down) for case 2.

 

[kuruman]

Normally I draw the diagram first and then solve the task, but I'm new to this site so I don't know how to fix it. In this case, you can observe it as I solved the math and then I drew the diagram. I believe you're looking at diagram 1 (m1 goes down) for case 2.

If you think that you understand what's going on, you can fix it by reposting a complete solution. That will summarize what has been discussed and will guide the thinking of anybody else you might have to solve this problem in the future.

I understand now, thank you so much!

Saying you understand and showing you understand are different things.

 

[Memo]

If you think that you understand what's going on, you can fix it by reposting a complete solution. That will summarize what has been discussed and will guide the thinking of anybody else you might have to solve this problem in the future.

Saying you understand and showing you understand are different things.

I can't find the edit option so I guess I just put it here