Particle in a cylindrically symmetric potential (Quantum mechanics)

[Stylord]

Homework Statement

Let $\rho , \phi , z$ be the cylindrical coordinates of a spinless particle ($x=\rho \times \cos(\phi) ,y=\rho \times \sin(\phi) ; \rho \geq 0 , 0 \leq \phi \lt 2\pi$. Assume that the potential energy of this particle depends only on $\rho$, and not on $\phi$ and z.
a. Write, in cylindrical coordinates, the differential operator associated with the Hamiltonian.Show that H commutes with Lz, and Pz.Show from this that the wave functions associated with the stationary states of the particle can be chosen in the form:
$\phi_{n,m,k}(\rho,\phi,z)=f_{n,m}(p) e^{im\phi} e^{ikz}$

Relevant Equations

See below

Hi, everyone.
Please check the following questions (extracted of the cohen Tanpoudji)

for the first question, here my Hamiltonian operator.

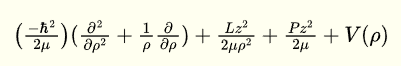
It's easy to see that it commutes with Lz and Pz.
Now we can determine a common eigenvector basis for these 3 operators.
For the angular part we need to solve
Lzg(théta,phi)=m$\hbar$g(théta,phi)(1)
Pzg(théta,phi)=k$\hbar$g(théta,phi)(2)
The resolution of the differential equation (1) and (2) gives us the angular part we see on the homework statement.
for the part $e^{im*\phi}$, the wave function needs to be continuous in all the space so $e^{2im*\pi}$=1,consequently, m need to be an integer
for the part $e^{ikz}$ I can't determine a condition and I don't know which values it can take.
So if someone have an hint thanks in advance !

 

[anuttarasammyak]

In z direction the state is free wave which has momentum eigenvalue and energy eigenvalue.
$$E=\frac{k^2\hbar^2}{2m}$$

 

[Stylord]

If the wave function was $e^{ikz}$ and if I injected this in the schrödinger equation, yes I will obtain this result. But the wavefunction is $e^{ikz}e^{im\phi}f(\rho)$ and if I write the eigenvalue equation of the Hamiltonian I will not obtain this, so I don't understand why we can say that. Could you enlighten me please ?

 

[vela]

For the part $e^{ikz}$, I can't determine a condition, and I don't know which values it can take.
So if someone have an hint thanks in advance!

There is no boundary condition that restricts the value of $k$.

 

[anuttarasammyak]

If the wave function was eikz and if I injected this in the schrödinger equation, yes I will obtain this result. But the wavefunction is eikzeimϕf(ρ) and if I write the eigenvalue equation of the Hamiltonian I will not obtain this, so I don't understand why we can say that. Could you enlighten me please ?

Hamiltonian is written as sum of
$$H=H(\rho,\phi)+H(z)$$
Wavefunction of energy eigenstate is written as product of
$$\psi=\eta(\rho,\phi)\xi(z)$$
$$H\psi =\xi H(\rho,\phi)\eta +\eta H(z)\xi=(E(\rho,\phi)+E(z))\xi \eta=(E(\rho,\phi)+E(z))\psi$$
Round quantum well in $\rho,\phi$ and free movement in z are independent. Sum of their energy is the system energy, e.g. ground state of the well and kinetic energy of $\frac{p_z^2}{2m}$.

 

[Stylord]

Ohhh it's a very good idea ! Now I Can finish the exercice, Thank you !