Particle on a ring (components in the postion basis)

[Lambda96]

Homework Statement

see screenshots

Relevant Equations

none

Hi,

I have problems with the task part b and g

To solve the task, we have received the following information

Task b

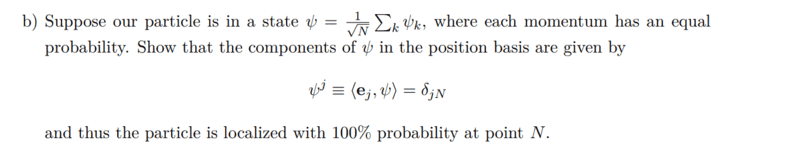
First, I wrote down what the state $\psi$ looks like

$$\psi=\frac{1}{\sqrt{N}} \sum\limits_{k}^{} \psi_k$$
$$\psi=\frac{1}{\sqrt{N}} \sum\limits_{k}^{} \frac{1}{\sqrt{N}} \sum\limits_{j}^{} e^{ikaj} \vec{e}_j$$

Then I to calculate $\psi^j=\braket{\vec{e}_j|\psi}$.

$$\braket{\vec{e}_j|\psi}=\vec{e}_j^{\dagger} \cdot \frac{1}{\sqrt{N}} \sum\limits_{k}^{} \frac{1}{\sqrt{N}} \sum\limits_{j}^{} e^{ikaj} \vec{e}_j$$

$$\braket{\vec{e}_j|\psi}=\vec{e}_j^{\dagger} \cdot \frac{1}{N} \sum\limits_{k}^{} \sum\limits_{j}^{} e^{ikaj} \vec{e}_j$$
Now I unfortunately do not know how to proceed further. But I don't understand, if all momentums are equally probable, why the particle should be 100% at location N and not at other locations like 1 and 2 and so on. What makes the point N so special that the particle should be there in contrast to the other points?

To solve task g, we have received the following information

Task g

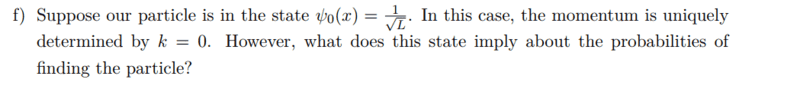
If I understood the task correctly, then the wave function is collapsed, to the eigenvector of the momentum operator, more precisely to $\psi_0$. The wave function has with 100% the eigenvalue of $\psi_0$ after the uncertainty principle, the uncertainty would have to become extremely large concerning the position, which means that the particle can be everywhere on the ring and thus the probability for each position is equally large.

 

[TSny]

$$\braket{\vec{e}_j|\psi}=\vec{e}_j^{\dagger} \cdot \frac{1}{\sqrt{N}} \sum\limits_{k}^{} \frac{1}{\sqrt{N}} \sum\limits_{j}^{} e^{ikaj} \vec{e}_j$$

In the second sum on the right, you should change the summation index $j$ to some other symbol so that the summation index is not confused with the $j$ in $\vec{e}_j^{\dagger}$. For example, you could write $$\braket{\vec{e}_j|\psi}=\vec{e}_j^{\dagger} \cdot \frac{1}{\sqrt{N}} \sum\limits_{k}^{} \frac{1}{\sqrt{N}} \sum\limits_{l}^{} e^{ikal} \vec{e}_l$$

 

[Lambda96]

Thanks TSny for your help , I have now changed the index of the summation from $j$ to $l$ and have now calculated the following.

$$\braket{\vec{e}_j|\psi}=\vec{e}_j^{\dagger} \cdot \frac{1}{\sqrt{N}} \sum\limits_{k}^{} \frac{1}{\sqrt{N}} \sum\limits_{l}^{} e^{ikal} \vec{e}_l$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \sum\limits_{k}^{} \sum\limits_{l}^{} e^{ikal} \vec{e}_j^{\dagger} \cdot \vec{e}_l$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \sum\limits_{k}^{} \sum\limits_{l}^{} e^{ikal} \delta_{jl}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \sum\limits_{k}^{} e^{ika} \delta_{j1}+e^{2ika} \delta_{j2}+ \ldots +e^{Nika} \delta_{jN}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \Bigl( e^{ia} \delta_{j1}+e^{2ia} \delta_{j2}+ \ldots +e^{Nia} \delta_{jN}+e^{2a} \delta_{j1}+e^{4ia} \delta_{j2}+ \ldots +e^{2Nia} \delta_{jN}+ \ldots + e^{Nia} \delta_{j1}+e^{2Nia} \delta_{j2}+ \ldots +e^{N^2ika} \delta_{jN} \Bigr)$$

$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \Bigl(\Bigl(e^{ia}+e^{2a} +\ldots+e^{Nia} \Bigr) \delta_{j1}+\Bigl( e^{2ia}+e^{4ia}+ \ldots +e^{2Nia} \Bigr)\delta_{j2}+ \ldots + \Bigl( e^{Nia}+e^{2Nia} + \ldots +e^{N^2ika} \Bigr)\delta_{jN}\Bigr)$$

Now I'm stuck

The individual entries in the brackets look almost like states $\vec{\psi}_k$, i.e.

$$\braket{\vec{e}_j|\psi}=\frac{1}{\sqrt{N}} \Bigl(\frac{1}{\sqrt{N}} \Bigl(e^{ia}+e^{2a} +\ldots+e^{Nia} \Bigr) \delta_{j1}+\frac{1}{\sqrt{N}} \Bigl( e^{2ia}+e^{4ia}+ \ldots +e^{2Nia} \Bigr)\delta_{j2}+ \ldots + \frac{1}{\sqrt{N}} \Bigl( e^{Nia}+e^{2Nia} + \ldots +e^{N^2ika} \Bigr)\delta_{jN}\Bigr)$$

$$\braket{\vec{e}_j|\psi}=\frac{1}{\sqrt{N}} \Bigl(\vec{\psi}_1 \delta_{j1}+\vec{\psi}_2 \delta_{j2}+ \ldots + \vec{\psi}_N \delta_{jN}\Bigr)$$

Now does it mean that if, for example, $\vec{e}_j=\vec{e}_2$, that only the state $\braket{\vec{e}_2|\psi}=\frac{1}{\sqrt{N}} \Bigl(\vec{\psi}_2 \delta_{22}\Bigr)$ remains and the particle is at location 2?

 

[TSny]

$$\braket{\vec{e}_j|\psi}=\frac{1}{N} \sum\limits_{k}^{} \sum\limits_{l}^{} e^{ikal} \delta_{jl}$$

Good. Consider the sum $$ \sum\limits_{l}^{} e^{ikal} \delta_{jl}$$Since $\delta_{jl}$ equals zero for any $l \neq j$, all of the terms in the summation are zero except for one term. So, the sum reduces to one term that can be written in terms of $k$, $a$, and $j$.

 

[Lambda96]

Thanks TSny for your help

Then I can write the term as follows

$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} \sum\limits_{l}^{}e^{ikal} \delta_{jl}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} e^{ikaj}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\Bigl( e^{iaj}+e^{2iaj}+e^{3iaj}+ \ldots +e^{Niaj} \Bigr)$$

 

[TSny]

$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} \sum\limits_{l}^{}e^{ikal} \delta_{jl}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} e^{ikaj}$$
$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\Bigl( e^{iaj}+e^{2iaj}+e^{3iaj}+ \ldots +e^{Niaj} \Bigr)$$

Good, except the sum over $k$ does not go from $k = 1$ to $k = N$. Recall that the values of $k$ are $k = 2\pi n /L$ for $n = 0, 1, 2, ... , N-1$.

 

[Lambda96]

Thanks again for your help TSny , also thanks for the hint with the index $k$

Could I then write the second line as follows?$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} e^{ikaj}$$

$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{n=0}^{N-1} e^{\frac{2i \pi n a j}{L}}$$

 

[TSny]

Thanks again for your help TSny , also thanks for the hint with the index $k$

Could I then write the second line as follows?$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{k}^{} e^{ikaj}$$

$$\braket{\vec{e}_j|\psi}=\frac{1}{N}\sum\limits_{n=0}^{N-1} e^{\frac{2i \pi n a j}{L}}$$

Yes, that looks right.

 

[Lambda96]

Thanks for your help TSny

 

[TSny]

You’re very welcome.