Particles moving on a regular hexagon

[Monsterboy]

Homework Statement

Six particles situated at the corners of a regular hexagon of side a move at $a$ constant speed $v$. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.

Relevant Equations

Speed = distance/time

When I first read the question, it didn't occur to me that these particles would ever meet or catch up with their neighbors. They are all traveling from one vertex to another with a velocity $v$ and a distance $a$, all either clockwise or anticlockwise right ?

The question says "Each particle maintains a direction towards the particle at the next corner." it's not clear if all the particles are moving around the center of the hexagon in the same direction (clockwise or anticlockwise) or whether some particles are moving towards each other.

If we consider two particles moving towards each other, we get $time = \frac{distance}{speed}$ so $t = \frac{\frac{a}{2}}{v}$

But the answer is $\frac{2a}{v}$

The question also says "Calculate the time the particles will take to meet each other." does this mean the all particles are going to meet each other ?
.

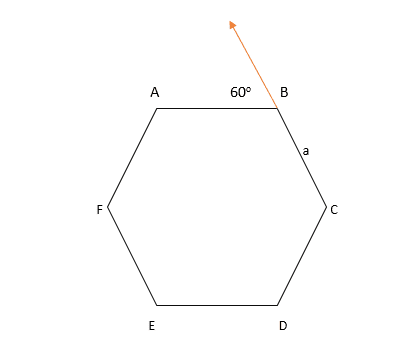
I saw one answer online which said for the particle at point C.
$velocity = v cos \theta = v cos 60 = \frac{v}{2}$
$t = \frac{a}{v/2} = \frac{2a}{v}$ but why would the particle at B stay there ? It would have moved to point A.

 

[Lnewqban]

The hexagon must simultaneously be shrinking and rotating.

 

[hutchphd]

This is a fun problem once you "see" it. Each particle chases the one in front, at speed v and always directed at the (moving) particle ahead all in the same direction. The key to the solution is to see that the particles continue to maintain a perfect hexagonal arrangement. Then you figure their relative speed using vectors. The result then follows as you describe.

 

[Steve4Physics]

@Lnewqban and @hutchphd beat me to it. But since I've already drafted it...

- the particles are all moving in the same sense (all clockwise or all anticlockwise).;

- each particle follows an inwards spiral path;

- the particles always form a hexagon, but the hexagon is rotating and shrinking;

- eventually all the particles reach the centre – that’s the moment they ‘meet each other’.

 

[Monsterboy]

Alright, so the hexagon is shrinking and rotating, but then all the particles are traveling at the same speed towards the next vertex.

When the particle at C has a velocity $v$ at a direction 60⁰ to the horizontal.
Its horizontal component will be $v\over 2$, this is less than the magnitude of $v$ that the next particle is traveling at, in the horizontal direction from point B to A.

So, the relative speed will be $v - \frac{v}{2} = \frac{v}{2}$.

As $a$ decreases, the relative speed remains the same ? And then at some point $a$ becomes zero that's when they meet right ?

For every 60⁰ rotation, the particles manage to move to the next vertex ?

I don't know how the answer can as simple as $\frac{2a}{v}$. For me looks like some kind of a summation, something where $a$ decreases from infinity(or any number) to zero and the magnitude of $v$ remains the same.

Can we calculate how many rotations it will take for the particles to meet each other in terms of $a$ and $v$?

 

[Lnewqban]

... I don't know how the answer can as simple as $\frac{2a}{v}$. For me looks like some kind of a summation, something where $a$ decreases from infinity(or any number) to zero and the magnitude of $v$ remains the same.

Can we calculate how many rotations it will take for the particles to meet each other in terms of $a$ and $v$?

Instead, place yourself on the center point of the rotating hexagon and focus your sight on one single particle.
Do you see the tangential speed of that particle?
If not, what type of movement, in what direction, and at what speed do you perceive?

Hint: Observing the geometry of one of the six triangles of the regular hexagon may reveal to you the reason for that number 2 in the correct answer.

 

[hutchphd]

Its simpler than that. You start a distance "a" from the particle ahead. You travel directly at it with relative speed v/2 as you have shown. How long to meet? Not a difficult calculation (in the appropriate reference frame!)

.

 

[Steve4Physics]

Can we calculate how many rotations it will take for the particles to meet each other in terms of $a$ and $v$?

That's an interesting question and presumably not part of the original homwork.

There is a constant angle (60º) between each particle's velocity and the particle's instantaneous radius of rotation. That means each particle moves along a logarithmic (equiangular) spiral.

The speed of rotation increases as the hexagon shrinks. In fact the angular speed tends to infinity as the 6 particles approach each other at the centre. So (I think) there will be an infinite number of rotations.

 

[hutchphd]

We have argued that the shape doesn't change, and the hexagon just gets smaller. Hence (as noted by @Steve4Physics this is a https://en.wikipedia.org/wiki/Logarithmic_spiralic_spiral and so scale change is equivalent to a rotation: "its spirals all the way down.."

 

[Monsterboy]

Hint: Observing the geometry of one of the six triangles of the regular hexagon may reveal to you the reason for that number 2 in the correct answer.

Well, its an equilateral triangle with sides of length $a$, that is rotating and shrinking. I don't know what else to make of it.

Its simpler than that. You start a distance "a" from the particle ahead. You travel directly at it with relative speed v/2 as you have shown. How long to meet? Not a difficult calculation (in the appropriate reference frame!)

.

If you are saying $time = \frac{distance}{speed}$ so, $t= \frac{a}{v/2} = \frac{2a}{v}$, I get that, but I can't visualize it. The particle ahead is not slowing down, nor is the particle chasing it speeding up, how are they ever going to meet if the particles are dimensionless and the hexagon shrinks forever ?

 

[haruspex]

the hexagon shrinks forever ?

No. Because the rotation accelerates they meet in a finite time.

 

[Monsterboy]

No. Because the rotation accelerates they meet in a finite time.

Okay but, Steve4Physics said

The speed of rotation increases as the hexagon shrinks. In fact the angular speed tends to infinity as the 6 particles approach each other at the centre. So (I think) there will be an infinite number of rotations.

If the particles meet in finite time, how can there be infinite rotations before they meet ?

 

[haruspex]

Okay but, Steve4Physics saidIf the particles meet in finite time, how can there be infinite rotations before they meet ?

Because the rotation rate increases geometrically. It's like 1+1/2+1/4+..., an infinite numbers of terms converging to a finite value.