mcastillo356
Gold Member
- 639
- 348
- Homework Statement
- Want to prove that, raised to an absolute value, monomials behave bounded
- Relevant Equations
- Variables raised to natural numbers in absolute value (for my purpose, I do not consider 0 as belonging to naturals)
On ##x\in{(-1,1)}##, ##x\in{\mathbb{R}}##, ##\forall{n\in{\mathbb{N}}}##, ##x^{|2n|}=O(x^{|2n+1|})##
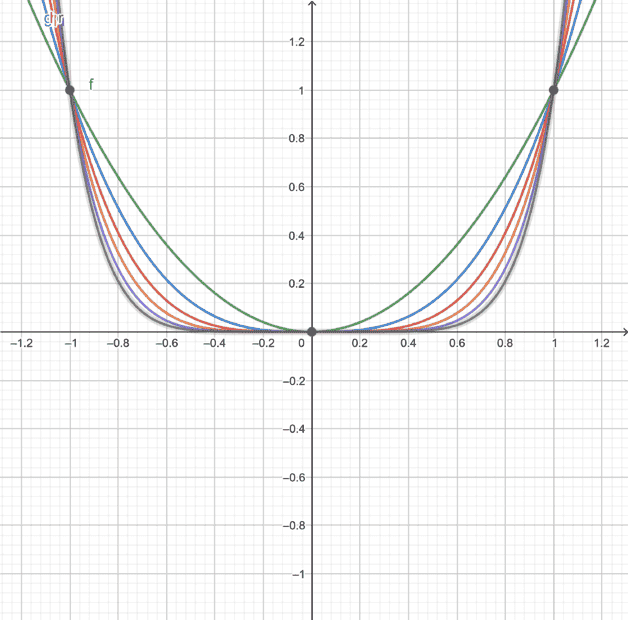
Sugestions? Any answer is wellcome!
Greetings, PF
Sugestions? Any answer is wellcome!
Greetings, PF