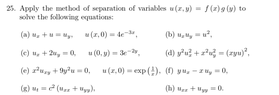Magnetons
- 22
- 3
- Homework Statement
- Apply the method of separation of variables ##u(x,y)=f(x)g(y)## to solve the equation .
- Relevant Equations
- ##u_{t}=c^{2}(u_{xx}+u_{yy})##
using the equation ##u(x,y)=f(x)g(y)##, first, I substitute the value of ##u_{xx}## and ##u_{yy}## in the given PDE. after that solve the ODEs but I can't understand about the ##u_{t}##.In my solution, I put ##u_{t}=0## because u is only the function of x and y. Is it the right approach, to me it seems wrong