- #1
BrettL789123
- 9
- 0
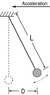
A pendulum has a length L = 1.14 m. It hangs straight down in a jet plane about to take off as shown by the dotted line in the figure. The jet accelerates uniformly, and during that time, the pendulum oscillates about the equilibrium position shown by the solid line, with D = 0.42 m. What is the acceleration of the plane?