- #1
MaZnFLiP
- 17
- 0
[SOLVED] Pendulum and Centripetal Motion Question
Picture and FBD
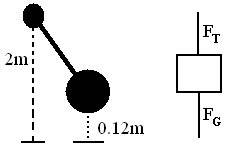
The Problem/Question
Calculate the speed of a 2.0m length pendulum at the very bottom of the swing if you raise it a vertical height of 0.12m
Relevant equations
[tex] F_net = F_T + F_G = F_C = m(\frac{V^2}{r}) [/tex]
The attempt at a solution
Well, after looking over this problem, I think I'm doing something amazingly wrong.
Looking at My equations, I went from
[tex] F_C = F_T + mg [/tex]
to
[tex] m(\frac{V^2}{r}) = F_T + mg [/tex]
From there I got:
[tex] \frac {V^2}{r} = F_T + g [/tex] because the masses cancel.
Next:
[tex] V^2 = gr + F_T[/tex]
After finding [tex](-9.81\frac{m}{s}^2)(2.0m) = 19.62[/tex], I found the square root which was [tex] 4.429 \frac {m}{s}^2 [/tex]
The problem is that after looking at the answer sheet, The answer is supposed to be:
[tex]1.5\frac{m}{s}^2[/tex]
Could someone please help as to tell me where I went wrong?
Picture and FBD
The Problem/Question
Calculate the speed of a 2.0m length pendulum at the very bottom of the swing if you raise it a vertical height of 0.12m
Relevant equations
[tex] F_net = F_T + F_G = F_C = m(\frac{V^2}{r}) [/tex]
The attempt at a solution
Well, after looking over this problem, I think I'm doing something amazingly wrong.
Looking at My equations, I went from
[tex] F_C = F_T + mg [/tex]
to
[tex] m(\frac{V^2}{r}) = F_T + mg [/tex]
From there I got:
[tex] \frac {V^2}{r} = F_T + g [/tex] because the masses cancel.
Next:
[tex] V^2 = gr + F_T[/tex]
After finding [tex](-9.81\frac{m}{s}^2)(2.0m) = 19.62[/tex], I found the square root which was [tex] 4.429 \frac {m}{s}^2 [/tex]
The problem is that after looking at the answer sheet, The answer is supposed to be:
[tex]1.5\frac{m}{s}^2[/tex]
Could someone please help as to tell me where I went wrong?