Pendulum on moving train

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

The problem and solution are,

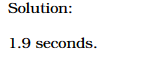
However, I don't understand why the answer is correct. I think that time should be dilated since $\Delta t = γ \Delta t_0 = 2γ$ where $γ \geq 1$ for $v \geq 0$.

Does anybody please know what I'm doing wrong here?

Thanks!

 

[Drakkith]

Is this the entire question? It seems to be missing some parts. Like, are they asking what Fred measures the period of the pendulum to be?

 

[member 731016]

Is this the entire question? It seems to be missing some parts. Like, are they asking what Fred measures the period of the pendulum to be?

Thank you for your reply @Drakkith!

Yes sorry, that is a typo of mine. It should also read: Which of the following is a possible measurement that Fred could make for the period of the pendulum?

Thanks!

 

[Drakkith]

Notice that Mo measured Fred's pendulum as having a 2.0 second period. That is, the pendulum is in the lab frame, not the train's frame. So that's the measured value with time dilation. What should the period be in Fred's frame? Shorter or longer than 2.0 seconds?

 

[member 731016]

Notice that Mo measured Fred's pendulum as having a 2.0 second period. That is, the pendulum is in the lab frame, not the train's frame. So that's the measured value with time dilation. What should the period be in Fred's frame? Shorter or longer than 2.0 seconds?

Thank you for your reply @Drakkith ! I think understand now, so as a general rule of thumb, the lab frame is always the frame with undiluted time, so is at rest?

Thanks!

 

[Drakkith]

I think understand now, so as a general rule of thumb, the lab frame is always the frame with undiluted time, so is at rest?

No, in this problem they are asking what is the period of the lab's pendulum when viewed from the train's reference frame. So you are treating the train as stationary and the lab as moving.

 

[Tom.G]

Doesn't the apparent speed depend on whether the pendulum and observer are approaching or receding from each other?
What am I missing?

 

[Drakkith]

Doesn't the apparent speed depend on whether the pendulum and observer are approaching or receding from each other?

For time dilation, no. The velocity is squared in the formula, so it's always a positive value even if the original velocity is negative.

 

[jbriggs444]

Doesn't the apparent speed depend on whether the pendulum and observer are approaching or receding from each other?
What am I missing?

The doppler shift depends on whether the source and receiver are approaching or receding. Doppler corresponds to the change in signal delay from one perceived pendulum swing to the next.

But the expected interpretation of "measure" in this problem is one where Mo has already cancelled out signal delay from his raw observations. He obtains the 2.0 second figure after accounting for that.

Based on the other questions that @ChiralSuperfields has been posting, it's all about the Lorentz transformations, length contraction and time dilation. The Lorentz transformations are about what happens once you have accounted for speed of light delays and have a coherent accounting for events in a chosen frame of reference. And then want to shift to another frame.