some bloke
- 283
- 99
- Homework Statement
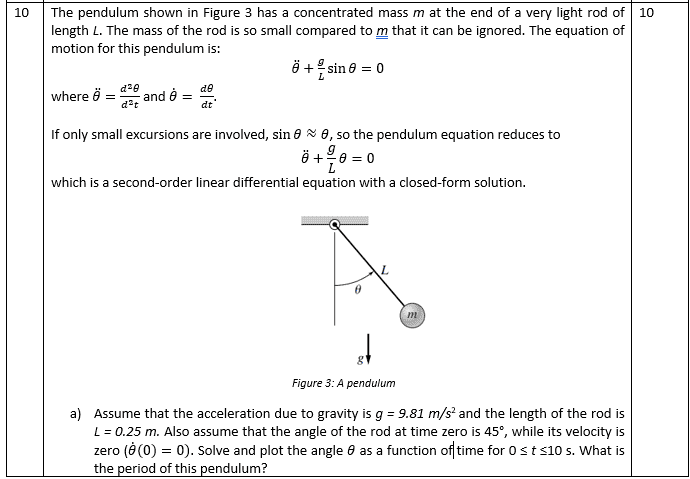
- The pendulum shown in Figure 3 has a concentrated mass m at the end of a very light rod of length L. The mass of the rod is so small compared to m that it can be ignored. The equation of motion for this pendulum is:
θ ̈+g/L sinθ=0
where θ ̈=(d^2 θ)/(d^2 t) and θ ̇= dθ/dt.
If only small excursions are involved, sinθ≈θ, so the pendulum equation reduces to
θ ̈+g/L θ=0
which is a second-order linear differential equation with a closed-form solution.
Assume that the acceleration due to gravity is g = 9.81 m/s2 and the length of the rod is L = 0.25 m. Also assume that the angle of the rod at time zero is 45°, while its velocity is zero (θ ̇(0)=0). Solve and plot the angle θ as a function of time for 0 ≤ t ≤10 s. What is the period of this pendulum?
What happens if the initial conditions are changed? Experiment with a 10°, then a 145° starting angle of the rod, considering initial velocity zero in both cases. Compare the period of oscillation with the theoretical period (hint: the angular frequency ω=√(g/L) ).
Suppose that the pendulum were moved to the top pf a mountain where the gravitation acceleration decreases to g = 9.6 m/s2. What would happen to the period of oscillation of the pendulum?
- Relevant Equations
- θ ̈+g/L sinθ=0, θ ̈+g/L θ=0
Apologies for my lack of knowledge on the equations front, I have burnt by brain out on this and haven't the capacity to learn LaTex right now! So here's a screengrab of it:
So, This is a Matlab coursework and I am struggling to work out how best to approach solving it. What I have so far is that:
(with D2 as the second Derivative and D as the first derivative)
D2=-g*sin(theta)/L, as given
D= integral of this, which is g*cos(theta)/L, and this is the angular velocity.
Therefore D = (981*cos(theta))/25)+C (simplified by Matlab into integers)
The question provides that at T=0, Theta = 45 and D=0, so I can say that C = -981*cos(45)/25.
I also know that at T=?, Theta = 0 and D is at it's maximum.
What I cannot fathom is how to get Theta as a function of Time out of this. I know that D is the angular velocity, so change in displacement over time, and I know that D2 is the angular accelleration, which is the change of velocity over time. I know that there's a way to do this, but I cannot dig far enough into my A-level maths of 9 years ago to find it. Helpfully, I've been advised that I will be taught how to do these things next year, after the coursework has been graded. Helpful.
Coding it into Matlab I can do, but I don't know what I'm coding. So, my biggest question is this: How to I get this strange equation of F''(theta)+f(theta)=0 to somehow give an answer in terms of t? Where does "t" come into it?
So, This is a Matlab coursework and I am struggling to work out how best to approach solving it. What I have so far is that:
(with D2 as the second Derivative and D as the first derivative)
D2=-g*sin(theta)/L, as given
D= integral of this, which is g*cos(theta)/L, and this is the angular velocity.
Therefore D = (981*cos(theta))/25)+C (simplified by Matlab into integers)
The question provides that at T=0, Theta = 45 and D=0, so I can say that C = -981*cos(45)/25.
I also know that at T=?, Theta = 0 and D is at it's maximum.
What I cannot fathom is how to get Theta as a function of Time out of this. I know that D is the angular velocity, so change in displacement over time, and I know that D2 is the angular accelleration, which is the change of velocity over time. I know that there's a way to do this, but I cannot dig far enough into my A-level maths of 9 years ago to find it. Helpfully, I've been advised that I will be taught how to do these things next year, after the coursework has been graded. Helpful.
Coding it into Matlab I can do, but I don't know what I'm coding. So, my biggest question is this: How to I get this strange equation of F''(theta)+f(theta)=0 to somehow give an answer in terms of t? Where does "t" come into it?