Pendulum with horizontal spring

[mountainbiker]

Homework Statement

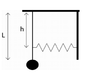
A 5kg sphere is connected to a thin massless but rigid rod of length L=1.3 m to form a simple pendulum. The rod is connected to a nearby vertical wall by a spring with a spring constant k= 75N/m, connected to it at a distance h=1.1 m below the pivot point of the pendulum. What is the angular frequency (in rad/s) of the system for small amplitude oscillations.

Homework Equations

\alpha = \omega²*\theta
I=m*r²
Torque=f*d*sin\theta

or small oscillations, sin\theta=\theta and cos\theta=1

The Attempt at a Solution

sum the torque and set them equal to \alphaI

gravitational torque= Lmg\theta

if theta is the angle between the rod and its equilibrium position, the angle of the spring torque is (theta + \pi/2), so the spring torque is
f*d*sin(theta + \pi/2). The force is k*\Deltax, or h*sin(theta + \pi/2) and the distance is h, giving

torque from spring =k*h²*sin\theta*sin(theta + \pi/2)
or k*h²*\theta*(theta + \pi/2)

My final equation is

mL²\omega²tex]\theta[/tex] = Lmg\theta + k*h²*\theta*(theta + \pi/2)

The problem is that this gives me a \omega that is dependant on \theta, which isn't possible. It should be constant. Can someone please tell me where I'm going wrong?

 

[ehild]

sin(theta+pi/2)= cos(theta). For small angles, cos(theta) =1.

ehild