- #1
Abourque72
- 6
- 2
I would like to preface this by saying that I solved the homework problem, but my professor gave me an added challenge of finding the period of the motion described in this problem.
1. Homework Statement
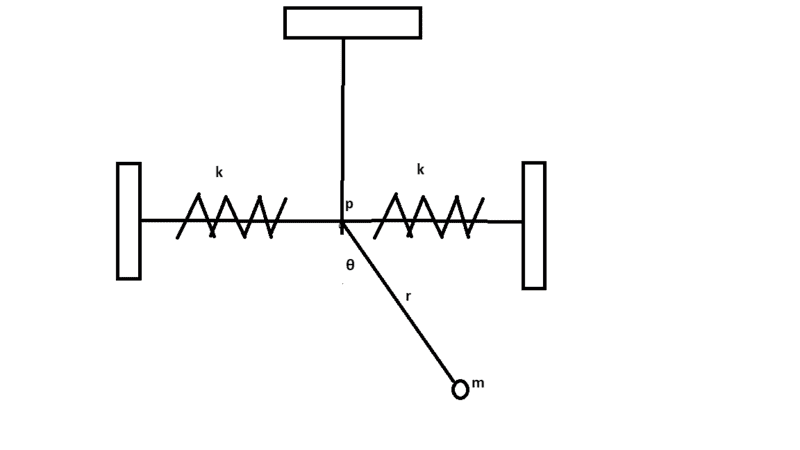
The pendulum bob of mass m shown in the figure below is suspended by an in-extensible string from point p. This point is free to move along a horizontal line under the action of the springs, each having an elastic constant k. Assume that point p is displaced a distance x to the right and then released; determine the equations of motion of the system.
I don't have an exact diagram so here's a replica with all necessary labels:
2. The Equations of Motion
After setting up the Lagrangian and finding the equations of motion (which have been checked by my professor), we get
$$m\ddot{x} + mr\ddot{\theta}\cos{\theta} - mr{\dot{\theta}}^2\sin{\theta} + 2kx = 0$$
$$\ddot{x} + r\ddot{\theta} + g\sin{\theta} = 0$$
First of all, we are assuming theta is very small. So far we have used an integral involving the mechanical and potential energy of a system to find the time it takes to travel from one position to another. The integral is essentially ##dt## written in terms of ##dx, E, V(x).## The problem is, I don't know what the maximum value of theta in this oscillation is. My professor thinks there is a way to make the period pop out of the equations under the small-angle approximations. After these approximations, I get
$$m\ddot{x} + mr\ddot{\theta} - mr{\dot{\theta}}^2\theta + 2kx = 0$$
$$\ddot{x} + r\ddot{\theta} + g\theta = 0$$
What immediately stood out to me was that both the ##x, \theta## accelerations could be canceled out in one step, giving ##2kx = m\theta(g + r{\dot{\theta}}^2)##. As I am writing this, I realize that separating the variables could be used here, and even better, that x can be written as an oscillator (duh).
So now I'm here:
$$\dot{\theta} = \sqrt{\frac{f(t)}{\theta} + C}$$ for some function of time ##f(t)## and some constant ##C##.
I don't know how to proceed, unless there is a way to solve this after finding f. Is there a more general way to do this given the equations of motion?
Thanks.
1. Homework Statement
The pendulum bob of mass m shown in the figure below is suspended by an in-extensible string from point p. This point is free to move along a horizontal line under the action of the springs, each having an elastic constant k. Assume that point p is displaced a distance x to the right and then released; determine the equations of motion of the system.
I don't have an exact diagram so here's a replica with all necessary labels:
2. The Equations of Motion
After setting up the Lagrangian and finding the equations of motion (which have been checked by my professor), we get
$$m\ddot{x} + mr\ddot{\theta}\cos{\theta} - mr{\dot{\theta}}^2\sin{\theta} + 2kx = 0$$
$$\ddot{x} + r\ddot{\theta} + g\sin{\theta} = 0$$
The Attempt at a Solution
First of all, we are assuming theta is very small. So far we have used an integral involving the mechanical and potential energy of a system to find the time it takes to travel from one position to another. The integral is essentially ##dt## written in terms of ##dx, E, V(x).## The problem is, I don't know what the maximum value of theta in this oscillation is. My professor thinks there is a way to make the period pop out of the equations under the small-angle approximations. After these approximations, I get
$$m\ddot{x} + mr\ddot{\theta} - mr{\dot{\theta}}^2\theta + 2kx = 0$$
$$\ddot{x} + r\ddot{\theta} + g\theta = 0$$
What immediately stood out to me was that both the ##x, \theta## accelerations could be canceled out in one step, giving ##2kx = m\theta(g + r{\dot{\theta}}^2)##. As I am writing this, I realize that separating the variables could be used here, and even better, that x can be written as an oscillator (duh).
So now I'm here:
$$\dot{\theta} = \sqrt{\frac{f(t)}{\theta} + C}$$ for some function of time ##f(t)## and some constant ##C##.
I don't know how to proceed, unless there is a way to solve this after finding f. Is there a more general way to do this given the equations of motion?
Thanks.
