Period of orbiting satellites - Mastering Physics 13.20

[xanthmode]

Homework Statement

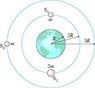
Three satellites orbit a planet of radius R, as shown in the figure. Satellites S_1 and S_3 have mass m. Satellite S_2 has mass 2 m. Satellite S_1 orbits in 250 minutes and the force on S_1 is 10,000 N.

See attached figure (knight_Figure_12_26.jpg).

a. What is the period of S_2? Answer: 250 min

b. What is the period of S_3?

c. What is the force on S_2? Answer: 2.00x10^4 N

d. What is the force on S_3?

e. What is the kinetic-energy ratio K_1/K_3 for S_1 and S_3? Answer: 2/3

Homework Equations

$$F=\frac{G m_1 m_2}{r^2}$$

$$T^2 = ( \frac{4 \pi ^2}{G M} ) r^3$$

The Attempt at a Solution

Parts (a) and (c) are obvious since mass does not effect the period and mass of S_2 is twice that of S_1 so it will have twice the force. The answer for (e) was also pretty easy since the only difference between the equations for the period would be the radius 2r vs. 3r.

I am having trouble with parts (b) and (d) due to a lack of information. I don't know the planet's radius or its mass. I can't see a way to substitute one equation into another to remove a variable either. I have too many unknowns and I just don't see a way to simplify it.

Any help would be greatly appreciated.

 

[Fightfish]

Can't see the attachment yet, but I'll hazard a guess...satellite 1 has an orbital radius of 2r while satellite 3 has an orbital radius of 3r based on what part of your answer, right?
Then the period of satellite 3 can be obtained from the 2nd equation you have via comparing it with the case for satellite 1 (since 4pi^2/GM is a constant). Just formulate the equation for both satellite 1 and satellite 3, then divide one of the equations by the other - the constant term cancels out.
A similar method can be done for (d)

 

[xanthmode]

Okay I got the answer for part (b) and I tried to do the same kind of operation for part (d) but The answer doesn't seem to work out.

$$F_1 = \frac{G m_1 m_2}{(2r)^2}$$

$$F_3 = \frac{G m_1 m_2}{(3r)^2}$$

$$\frac{F_1}{F_3} = \frac{\frac{G m_1 m_2}{(2r)^2}}{\frac{G m_1 m_2}{(3r)^2}}$$

$$\frac{F_1}{F_3} = \frac{3^3}{2^3}$$

...and $$F_1 = 10000$$ so...

$$F_3 = 10000 \frac{8}{27} = 2963$$

But Mastering Physics says this is wrong. See anything wrong?

 

[xanthmode]

Screwed up the force equation in the last few steps. The denominator should be r^2 rather than r^3. Thanks so much for your help Fightfish.