DaveC426913
Gold Member
- 23,926
- 7,978
- TL;DR Summary
- Is this graph spiral or merely polar?
Could someone explain the geometry of this graph?
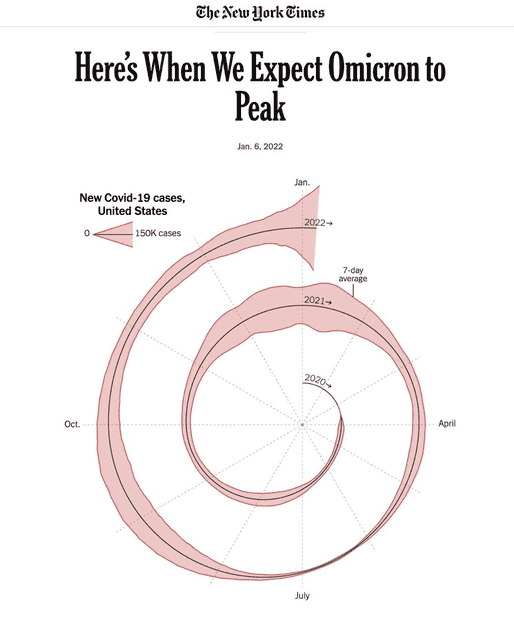
- Why does the radial distance vary non-uniformly? To-wit: Distance from origin to Nov 2020 is much larger than Nov 2020 to Nov 2021
- Why are there two areas - one above and one below - the centre line?
