Perpendicular Bisector of a triangle

[nmnna]

Homework Statement

$ABC$ is a triangle such that $\angle ABC = 37^{\circ}15'$, $\angle ACB = 59^{\circ}40'$, $BC = 8$ cm; the perpendicular bisector of $BC$ cuts $BA$, $CA$ produced at $P, \ Q$. Find the length of $PQ$.

Relevant Equations

$\tan(\alpha) = \frac{opposite \ side}{adjacent \ side}$

Here is my attempt to draw a diagram for this problem:

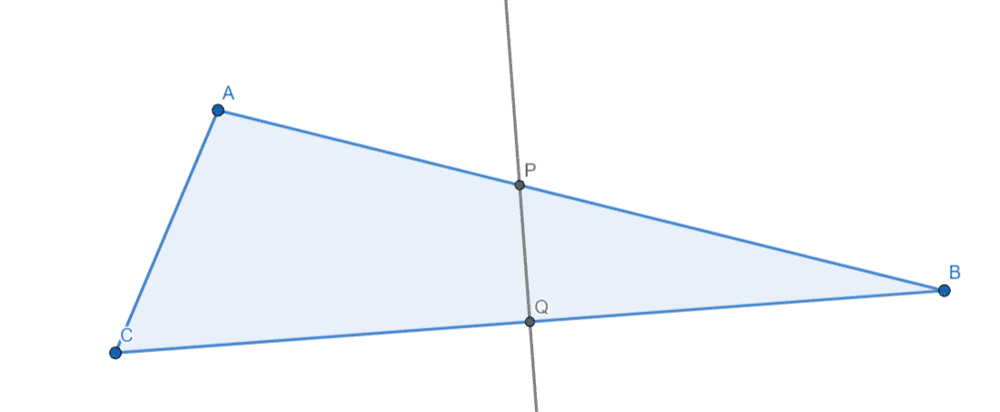
I'm confused about the "the perpendicular bisector of $BC$ cuts $BA$, $CA$ produced at $P, \ Q$" part of the problem.
How does perpendicular bisector of $BC$ cut the side $CA$?

 

[mjc123]

It cuts CA produced. Extend the line CA until it meets the bisector. That point is Q (not where you have put it).

 

[nmnna]

It cuts CA produced. Extend the line CA until it meets the bisector. That point is Q (not where you have put it).

Thank you

 

[nmnna]

It cuts CA produced. Extend the line CA until it meets the bisector. That point is Q (not where you have put it).

I changed my diagram.
Now I have the right triangle $\triangle PQC$, where $CP = 4$cm (since $PQ$ is a perpendicular bisector), $\angle QCP = 59^{\circ}40'$, so I can find $PQ$ using the relation $$\tan\angle QCP = \frac{PQ}{CP}$$
I got $\approx 6.818$ which is not the answer given in my textbook. Where did I go wrong?

 

[Lnewqban]

View attachment 280723
I changed my diagram.
Now I have the right triangle $\triangle PQC$, where $CP = 4$cm (since $PQ$ is a perpendicular bisector), $\angle QCP = 59^{\circ}40'$, so I can find $PQ$ using the relation $$\tan\angle QCP = \frac{PQ}{CP}$$
I got $\approx 6.818$ which is not the answer given in my textbook. Where did I go wrong?

The description seems confusing to me as well.
Could it be that point P should be located where the perpendicular bisector of BC cuts BA?
What is the answer given in your textbook?
If it is close to 3.75 cm, then your last diagram is not correct regarding location of P.

 

[mjc123]

P is the point you have called L. The original statement, which is perhaps not as clear as it might be, means "the perpendicular bisector of BC cuts BA at P and cuts CA produced at Q."

 

[nmnna]

P is the point you have called L. The original statement, which is perhaps not as clear as it might be, means "the perpendicular bisector of BC cuts BA at P and cuts CA produced at Q."

Thank you for your help.