- #1
NODARman
- 57
- 13
- Homework Statement
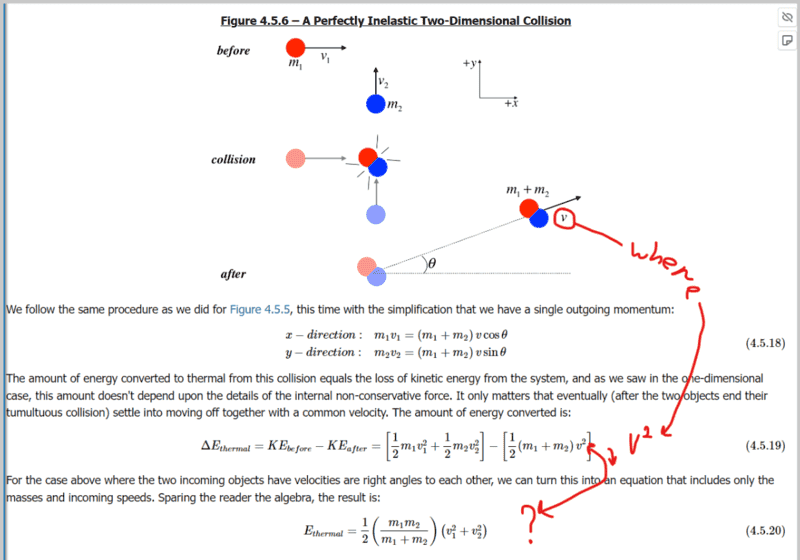
- Where did "v" go?
- Relevant Equations
- .
I still don't get it where did "v" go.
I'm trying to solve the problem that is on the second image.
Second image.

I'm trying to solve the problem that is on the second image.
Second image.