MHB Perpendicular lines and the product of their slopes

[MarkFL]

As students taking pre-calculus, you are probably aware that when two lines are perpendicular, the product of their slopes is -1. Let's see why this is.

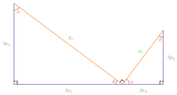
Let one line be $\displaystyle y_1=m_1x+b_1$ and the other line be $\displaystyle y_2=m_2x+b_2$.

Now,we know the angle of inclination of a line is found from:

$\displaystyle m=tan(\theta)\,\therefore\,\theta=\tan^{-1}(m)$

Let $\displaystyle \theta_1$ be the angle of inclination of $\displaystyle y_1$ and $\displaystyle \theta_2$ be the angle of inclination of $\displaystyle y_2$.

Now, suppose $\displaystyle 0\le\theta_2\le\frac{\pi}{2}$ and $\displaystyle -\frac{\pi}{2}\le\theta_1\le0$.

If the two lines are perpendicular, then we must have:

$\displaystyle \theta_2=\theta_1+\frac{\pi}{2}$

Now, taking the tangent of both sides, we find:

$\displaystyle \tan\left(\theta_2 \right)=\tan\left(\theta_1+\frac{\pi}{2} \right)$

Using the identity $\displaystyle \tan\left(x+\frac{\pi}{2} \right)=-\cot(x)$ we have:

$\displaystyle \tan\left(\theta_2 \right)=-\cot\left(\theta_1 \right)$

$\displaystyle \tan\left(\theta_2 \right)=-\frac{1}{\tan\left(\theta_1 \right)}$

And so, we must then have:

$\displaystyle m_2=-\frac{1}{m_1}$

$\displaystyle m_1m_2=-1$

Comments and questions should be posted here:

http://mathhelpboards.com/commentary-threads-53/commentary-perpendicular-lines-product-their-slopes-4218.html

 

[MarkFL]

This topic is for commentary pertaining to the tutorial:

http://mathhelpboards.com/math-notes-49/perpendicular-lines-product-their-slopes-2953.html

 

[MarkFL]

Here's another method using similarity. Consider the following diagram:

View attachment 8299

We can see that the slope of line $y_1$ is $$m_1=-\frac{\Delta y_1}{\Delta x_1}$$ and the slope of line $y_2$ is $$m_2=\frac{\Delta y_2}{\Delta x_2}$$

By similarity, we have:

$$\frac{\Delta y_1}{\Delta x_1}=\frac{\Delta x_2}{\Delta y_2}\implies \frac{\Delta y_1}{\Delta x_1}\cdot\frac{\Delta y_2}{\Delta x_2}=1$$

Hence:

$$m_1m_2=-\frac{\Delta y_1}{\Delta x_1}\cdot\frac{\Delta y_2}{\Delta x_2}=-1$$

 

[Ackbach]

Your second method is very fast! I remember coming up with my own proof using vectors and dot products, but it took a whole page. Your second method, it seems to me, has a good deal of pedagogical value.

 

[MarkFL]

Your second method is very fast! I remember coming up with my own proof using vectors and dot products, but it took a whole page. Your second method, it seems to me, has a good deal of pedagogical value.

Thank you...I stumbled upon that helping a student at another site to find the third vertex of a right triangle, when given two of the vertices in the plane, and the leg lengths. When I realized I had found a nice method to show the product of the slopes of perpendicular lines is -1, I raced here to add it to this topic. :D