Perturbation treatment of hydrogen molecular ion

[patric44]

Homework Statement

question about perturbation method treatment ?

Relevant Equations

in the pictures

hi guys
i am a the third year undergrad student and in this 2nd semester in my collage we should start taking quantum mechanics along with
molecular physics , our molecular physics professor choose a book that we are going to take which is " molecular physics by wolfgang Demtroder "
when i opened that book i found that it uses some advanced quantum mechanics like perturbation theory ... i found it really heavy for a student that just has some relativity intermediate quantum mechanics knowledge !
i started to get this perturbation theory thing ! but has some questions about this :
i get that he can represent the electronic distribution as a linear combination of functions with some coefficients that depend on the
position of the nuclei , how did he expand that integral and reached that partial derivative term its very unclear to me ?

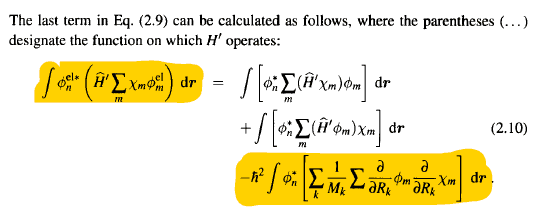
i appreciate any help
thanks

 

[TSny]

Can you give us the explicit expression for the operator $\hat H'$?

 

[patric44]

 

[TSny]

This tells you that $\hat{H'}$ is the operator corresponding to the kinetic energy due to the motion of all of the nuclei. Suppose the $k^{th}$ nucleus has a mass $M_k$ and position $\mathbf R_k$. Can you write down the kinetic energy operator $\hat T_k$ for this nucleus?

 

[patric44]

This tells you that $\hat{H'}$ is the operator corresponding to the kinetic energy due to the motion of all of the nuclei. Suppose the $k^{th}$ nucleus has a mass $M_k$ and position $\mathbf R_k$. Can you write down the kinetic energy operator $\hat T_k$ for this nucleus?

I guess it should be something like this :

I'm not sure if the laplacian expression in spherical is right because the book didn't mention the angles in his treatment!

 

[TSny]

Let's express the laplacians in cartesian coordinates and see if we can make sense of (2.10).

So, as you wrote, $\hat{H'} = \sum_k \frac{1}{M_k} \nabla_k^2$.

If $x_k$, $y_k$, and $z_k$ denote the cartesian coordinates of the position of the $k^{th}$ nucleus, what does $\hat{H'}$ look like when expressed in terms of these coordinates?

Also, suppose you have two functions $f(x)$ and $g(x)$. Expand the expression $\frac{d^2}{dx^2}\left[f(x)g(x)\right]$.

 

[patric44]

Let's express the laplacians in cartesian coordinates and see if we can make sense of (2.10).

So, as you wrote, $\hat{H'} = \sum_k \frac{1}{M_k} \nabla_k^2$.

If $x_k$, $y_k$, and $z_k$ denote the cartesian coordinates of the position of the $k^{th}$ nucleus, what does $\hat{H'}$ look like when expressed in terms of these coordinates?

Also, suppose you have two functions $f(x)$ and $g(x)$. Expand the expression $\frac{d^2}{dx^2}\left[f(x)g(x)\right]$.

I guess something like this :

 

[TSny]

OK. Generalize this to get an expansion of

$\nabla_k^2 \left[f(\mathbf R_k) g(\mathbf R_k)\right]$

 

[patric44]

OK. Generalize this to get an expansion of

$\nabla_k^2 \left[f(\mathbf R_k) g(\mathbf R_k)\right]$

I guess some terms should vanish as they are not differentiable with respect to either x,y,z?

 

[TSny]

I guess some terms should vanish as they are not differentiable with respect to either x,y,z?

In the expression $f(\mathbf R_k)$, $\mathbf R_k$ is the position vector of the $k^{th}$ molecule: $\mathbf R_k = x_k \hat i +y_k \hat j+z_k \hat k$. The notation $f(\mathbf R_k)$ is just shorthand for $f(x_k, y_k, z_k)$.

In your result for $\nabla_k^2 \left[f(\mathbf R_k) g(\mathbf R_k)\right]$, your use of primes might be a little confusing. But I guess your subscripts, $x$, $y$, and $z$ indicate what derivative the prime denotes.

Can you tidy up your result for $\nabla_k^2 (fg)$ by expressing it in terms of $\nabla_k^2 f$, $\nabla_k^2 g$, $\vec \nabla_k f$ and $\vec \nabla_k g$?

 

[patric44]

In the expression $f(\mathbf R_k)$, $\mathbf R_k$ is the position vector of the $k^{th}$ molecule: $\mathbf R_k = x_k \hat i +y_k \hat j+z_k \hat k$. The notation $f(\mathbf R_k)$ is just shorthand for $f(x_k, y_k, z_k)$.

In your result for $\nabla_k^2 \left[f(\mathbf R_k) g(\mathbf R_k)\right]$, your use of primes might be a little confusing. But I guess your subscripts, $x$, $y$, and $z$ indicate what derivative the prime denotes.

Can you tidy up your result for $\nabla_k^2 (fg)$ by expressing it in terms of $\nabla_k^2 f$, $\nabla_k^2 g$, $\vec \nabla_k f$ and $\vec \nabla_k g$?

Thank you so much
I guess the final expression should be as this :

Thanks again that helped me a lot, I thought that I would never get this scary looking equation

 

[patric44]

I'm beginning to like perturbation theory

 

[TSny]

You just about have it. You even included the summation over $m$ in the last term, which the text left out.

However, the argument of your summations in the last term is not written quite correctly. As written, you would have "cross terms" like $\frac{\partial \phi_m}{\partial x_k} \frac{\partial \chi_m}{\partial y_k}$ which have derivatives with respect to $x_k$ and $y_k$ in the same term. But your result in post #9 did not have such mixed terms in $x_k$ and $y_k$. Try to express your last integral in terms of the gradients $\vec \nabla_k \phi$ and $\vec \nabla_k \chi$.

We strongly encourage posters to type out mathematical expressions (using Latex if possible) rather than posting pictures of handwritten work. I should have mentioned this much earlier. Typing your expressions makes it much easier for helpers to quote specific parts of your work.

 

[patric44]

You just about have it. You even included the summation over $m$ in the last term, which the text left out.

However, the argument of your summations in the last term is not written quite correctly. As written, you would have "cross terms" like $\frac{\partial \phi_m}{\partial x_k} \frac{\partial \chi_m}{\partial y_k}$ which have derivatives with respect to $x_k$ and $y_k$ in the same term. But your result in post #9 did not have such mixed terms in $x_k$ and $y_k$. Try to express your last integral in terms of the gradients $\vec \nabla_k \phi$ and $\vec \nabla_k \chi$.

We strongly encourage posters to type out mathematical expressions (using Latex if possible) rather than posting pictures of handwritten work. I should have mentioned this much earlier. Typing your expressions makes it much easier for helpers to quote specific parts of your work.

I almost had it, I think the confusing part that the book express all the derivative as d/dR, but I guess I has it right this time :

I'm really sorry for not using Latex but I really don't know how to, I will learn it an I promise you that the next perturbation theory question will be in latex

 

[patric44]

The next summation should be on "m", my bad

 

[TSny]

Looks good!