- #1
spaghetti3451
- 1,344
- 34
The following is taken from page 5 of Peskin and Schroeder. It talks about the computation of ##\mathcal{M}## for the annihilation reaction ##e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}##.
Even for this simplest of QED processes, the exact expression for ##\mathcal{M}## is not known. Actually this fact should come as no surprise, since even in nonrelativistic quantum mechanics, scattering problems can rarely be solved exactly. The best we can do is obtain a formal expression for ##\mathcal{M}## as a perturbation series in the strength of the electromagnetic interaction, and evaluate the first few terms in this series.
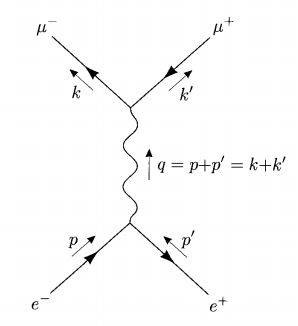
Feynman has invented a beautiful way to organize and visualize the perturbation series: the method of Feynman diagrams. Roughly speaking, Feynman diagrams display the flow of electrons and photons during the scattering process. For our particular calculation, the lowest-order term in the perturbation series can be represented by a single diagram, shown below. The diagram is made up of external lines (representing the four incoming and outgoing particles), internal lines (representing virtual particles, in this case one virtual photon), and vertices. Straight lines are used for fermions and wavy lines are used for photons. The arrows on the straight lines denote the direction of negative charge flow, not the direction of momentum. A ##4##-momentum vector is assigned to each external line. The momentum ##q## of the one internal line is determined by momentum conservation at either of the vertices: ##q=p+p'=k+k'##. A spin state (either up or down) must also be associated with each external fermion.
I have the following questions regarding the above two paragraphs:
Even for this simplest of QED processes, the exact expression for ##\mathcal{M}## is not known. Actually this fact should come as no surprise, since even in nonrelativistic quantum mechanics, scattering problems can rarely be solved exactly. The best we can do is obtain a formal expression for ##\mathcal{M}## as a perturbation series in the strength of the electromagnetic interaction, and evaluate the first few terms in this series.
Feynman has invented a beautiful way to organize and visualize the perturbation series: the method of Feynman diagrams. Roughly speaking, Feynman diagrams display the flow of electrons and photons during the scattering process. For our particular calculation, the lowest-order term in the perturbation series can be represented by a single diagram, shown below. The diagram is made up of external lines (representing the four incoming and outgoing particles), internal lines (representing virtual particles, in this case one virtual photon), and vertices. Straight lines are used for fermions and wavy lines are used for photons. The arrows on the straight lines denote the direction of negative charge flow, not the direction of momentum. A ##4##-momentum vector is assigned to each external line. The momentum ##q## of the one internal line is determined by momentum conservation at either of the vertices: ##q=p+p'=k+k'##. A spin state (either up or down) must also be associated with each external fermion.
I have the following questions regarding the above two paragraphs:
- Why is the perturbation series called a formal expression?
- What is the original Hamiltonian and the interaction Hamiltonian for this problem?
- What is the expression for the strength of the electromagnetic interaction?
- Why is the perturbation series obtained in the strength of the electromagnetic interaction? Can't we obtain the perturbation series in the order of some other quantity?