Phase difference between two light waves of the same frequency

[hello478]

Homework Statement

Two light waves of the same frequency are represented by the diagram.


What could be the phase difference between the two waves?

A 150°
B 220°
C 260°
D 330°

Relevant Equations

phase difference = phase angle in this diagram...

the diagram.

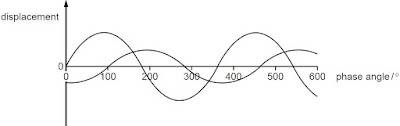
i found that the phase difference between them is 100º
but how is the answer 260
can someone please explain?

 

[BvU]

Since 100 is not in the list, you need to pick another. And there is a best candidate.

 

[hello478]

Since 100 is not in the list, you need to pick another. And there is a best candidate.

is it 150º ? because it is the closest to 100º

 

[BvU]

Guessing, are we?
It is not 150, you already have the correct answer as quoted in #1

 

[hello478]

Guessing, are we?
It is not 150, you already have the correct answer as quoted in #1

i dont know how it came to be the answer...

 

[BvU]

As a useful exercise you could draw 4 graphs, each with two waves. The first one with a phase difference of150 degrees, the others with 220, 260 and 330

 

[hello478]

As a useful exercise you could draw 4 graphs, each with two waves. The first one with a phase difference of150 degrees, the others with 220, 260 and 330

drawing them, give me 5 mins and ill get back to you

 

[hello478]

this is what i got for 260º
what next??

As a useful exercise you could draw 4 graphs, each with two waves. The first one with a phase difference of150 degrees, the others with 220, 260 and 330

 

[hello478]

this one is for 220º

 

[hello478]

i still dont understand it... :(

 

[haruspex]

i still dont understand it... :(

The curves are $\sin(\theta+\phi_1)$ and $\sin(\theta+\phi_2)$.
Suppose $\phi_1+2\pi>\phi_2>\phi_1$. The phase difference is $\phi_2-\phi_1$.
But $\sin(\theta+\phi_1)=\sin(\theta+\phi_1+2\pi)$, so those are two representations of the same wave. So we could equally say the phase difference is $\phi_1+2\pi-\phi_2$.

 

[Orodruin]

If the phase difference between the first and the second is 100°, what is the phase difference between the second and first?

 

[Steve4Physics]

i still dont understand it... :(

My two-pennies-worth…

On the Post 1# diagram, call the larger-amplitude wave ‘A’ and the smaller-amplitude wave ‘B’.

A passes through (0, 0). The next 'matching' point on B is (100º,0). So the phase difference is (100 – 0 =) 100º.

But you could equally well say:

B passes through (100º, 0). The next 'matching' point on A is (360º, 0). So the phase difference is (360-100=) 260º.

Remember that an angle of (say) +260º is the same as an angle of -100º. You can choose which wave (A or B) is the reference.