Phase Shift of IGMF Band-Pass Filter at Corner Freq: Solved Problem

[roam]

Homework Statement

I need some help understanding how the phase shift was calculated in the following solved problem:

Shown below is an IGMF band-pass filter:

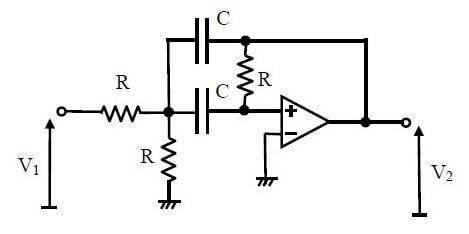
Its transfer function is given by: $\frac{V_2}{V_1}=\frac{-\omega_0}{\sqrt{2}} \frac{s}{s^2+\sqrt{2} \omega_0 s + \omega_0^2}$ where $\omega_0 = \frac{\sqrt{2}}{RC}$

Calculate the gain (in dB) and phase shift of the filter at the corner frequency $\omega_0$.

Solution:

$\frac{V_2}{V_1}(\omega_0) = - \frac{1}{RC} \frac{j \omega_0}{\sqrt{2} j \omega_0^2} = - \frac{-1}{RC} \frac{1}{\sqrt{2} \omega_0} = - \frac{1}{2}$

$\implies |\frac{V_2}{V_1} (\omega_0)| = 20 \log(1/2) = -6 \ dB$,

$phase |\frac{V_2}{V_1}(\omega_0)|= \pi$

So how did they work out the phase shift to be π?

The Attempt at a Solution

What formula have they used to find the phase shift?

I couldn't find any notes in my coursebook on finding phase shift once you have the gain. Any help or explanation is greatly appreciated.

 

[CWatters]

I'm a bit rusty but as I recall you..

1) Replace s with jω
2) Re-write the transfer function in the form Re(ω) + jIm(ω) where Re(ω) and Im(ω) are the real and imaginary parts.
3) The gain is Sqrt{Re(ω)² + Im(ω)²}
4) The phase is Tan^-1{Im(ω)/Re(ω)}

 

[roam]

I'm a bit rusty but as I recall you..

1) Replace s with jω
2) Re-write the transfer function in the form Re(ω) + jIm(ω) where Re(ω) and Im(ω) are the real and imaginary parts.
3) The gain is Sqrt{Re(ω)² + Im(ω)²}
4) The phase is Tan^-1{Im(ω)/Re(ω)}

Thank you for your input, but they ask for phase shift at the corner frequency ω₀. At this frequency the transfer function reduces to $-1/2$, the imaginary part is zero... so $tan^{-1} (0)=0$. This is wrong.

Did you get $\pi$ using this method?

A textbook gives the formula:

$\phi_k = \frac{\pi}{n} \left( k- \frac{1}{2} \right)$

I've attached the formula page to this post. I'm not sure if this is the right formula, it is given for VCVS circuits (I'm not sure if it also holds for IGMF configurations).

I used the value $n=1$ (first order filter). If I use $k=-1/2$ I get $\phi = - \pi$, and if I use $k=n/2 = 1/2$ I will get $\phi = 0$. Is this the right equation to use, and what k should I be using?

 

[NascentOxygen]

A pure inversion is a phase shift of 180°

For a bandass filter, ωo is normally referred to as the centre frequency, not the corner frequency.

 

[roam]

A pure inversion is a phase shift of 180°

For a bandass filter, ωo is normally referred to as the centre frequency, not the corner frequency.

But what equation did they use to get the 180° in this problem? I'm a bit confused... once we have the gain from the transfer function at a particular frequency, what formula do we use to find the phase shift?

 

[AlephZero]

Think about the difference between a gain of +1/2 and -1/2. One has the input and output in phase, the other has them 180° out of phase.

The "formula" Tan-1{Im(ω)/Re(ω)} is a bit misleading, because for any given values of Im(ω) and Re(ω) it always gives you two possible answers, 180° apart. You need to draw a diagram to see which quadrant the angle is in, depending on whether Im(ω) and Re(ω) are positive or negative.

 

[roam]

Yes, and this is what I've done:

First I've substituted the frequency of interest ω₀ into the transfer function, and I've got a gain of +1/2. So Re(ω) is positive, whereas Im(ω)=0, right?

I used the tangent formula to find the phase shift:

$\phi=tan^{-1} (Im/Re) = tan^{-1} (0/(1/2))=0$

So why do I get the wrong answer?

We would always get $\phi(0)=0°$ and $\phi(\infty)=90°$ (or other values in other cases, etc).

So how can I possibly get -π using this formula when the imaginary part is 0?

 

[NascentOxygen]

Yes, and this is what I've done:

First I've substituted the frequency of interest ω₀ into the transfer function, and I've got a gain of +1/2.

The formula in your first post in this thread shows a gain of -1/2. So which is it??

tan 180 = 0
tan 0 = 0

So you need to look at the sign of the real component to see which side of the x-axis it lies.

 

[roam]

The formula in your first post in this thread shows a gain of -1/2. So which is it??

tan 180 = 0
tan 0 = 0

So you need to look at the sign of the real component to see which side of the x-axis it lies.

Thank you. Oops, sorry I meant -1/2. So basically every time the imaginary part is 0 and we have a negative or positive gain, the phase will be $-180°$ or $180°$ respectively? Is this right?

I'm still not 100% sure why the sign of gain determines the location of $\phi$ on the tangent graph.

 

[NascentOxygen]

Thank you. Oops, sorry I meant -1/2. So basically every time the imaginary part is 0 and we have a negative or positive gain, the phase will be $-180°$ or $180°$ respectively? Is this right?

No.

-180° and +180° are equivalent.

Negative gain at 0° is equivalent to positive gain with 180° phase shift. For a sinewave you'll see no difference between the two.

 

[donpacino]

Using methods previously mentioned can get you the exact phase at any frequency. However there is an easy way to determine the approximately phases at different points.

A zero will always add a positive phase shift of 90 degrees.
A pole will always add a negative phase shift of 90 degrees.

The effect of the pole/zero on face begins 1 decade before the pole/zero, and ends 1 decade after the pole/zero.

if there is a pole/zero that is equal to zero, that is the phase of the system at DC.

So the circuit you posted has a zero at 0 and 2 poles at (1\pmj)*wo/sqrt(2)
that means the phase will start at 90. It will begin breaking about 1 decade before wo, and end breaking 1 decade after wo. each pole will effect the phase by 90 degrees, the the phase will be -90 1 decade after the break point