Phase velocity in oblique Angle propagation (Plane wave)

[baby_1]

Homework Statement

Maxwell equation

Relevant Equations

V=xt

Hello,
Regarding the wave oblique angle propagation and based on Balanis "Advanced engineering Electromagnetic" book on page 136 ( it has been attached) I need to know why the phase velocity in x direction is not important to keep in step with a constant phase plane( Just equation 4-23).

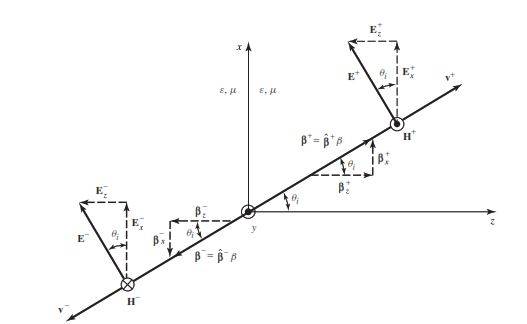I derived the electric filed:
\vec{E}=E_{x}(z)e^{-j\beta (xSin(\theta )+zCos(\theta ))}
For calculating the phase velocity we need to obtain the time-domain form:
\vec{E(t)}=Re\{E_{x}(z)e^{-j\beta (xSin(\theta )+zCos(\theta ))}e^{jwt}\}=E_{x}(z)Cos(\omega t-\beta (xSin(\theta )+zCos(\theta ))
Calculating the Z- phase velocity (X=0):
\frac{d}{dt}(\omega t-\beta zCos(\theta ))=0=>\omega -\beta \frac{dz}{dt}Cos(\theta )=0=>v_{z}=\frac{\omega}{\beta Cos(\theta )}
which is the same as the book. However,

1)First: I need to know why the x velocity (on x-axis) is not important.
x phase velocity:(z=0)
\frac{d}{dt}(\omega t-\beta xSin(\theta ))=0=>\omega -\beta \frac{dx}{dt}Sin(\theta )=0=>v_{x}=\frac{\omega}{\beta Sin(\theta )}
2)Second: Why the resultant phase velocity is not the same as the light velocity(v_{c}=\frac{\omega}{\beta})
\sqrt{v_{z}^2+v_{x}^2}=\sqrt{({\frac{\omega}{\beta Cos(\theta )})}^2+({\frac{\omega}{\beta Sin(\theta )})}^2}=(\frac{\omega}{\beta Sin(2*\theta )})

 

[TSny]

1)First: I need to know why the x velocity (on x-axis) is not important.

The "x velocity" is just as important as the "z velocity". I guess that the textbook just decided not to mention the x velocity since it can be found in a similar manner to the z velocity. Below, I denote these velocities as $u_x$ and $u_z$.

2)Second: Why the resultant phase velocity is not the same as the light velocity(v_{c}=\frac{\omega}{\beta})
\sqrt{v_{z}^2+v_{x}^2}=\sqrt{({\frac{\omega}{\beta Cos(\theta )})}^2+({\frac{\omega}{\beta Sin(\theta )})}^2}=(\frac{\omega}{\beta Sin(2*\theta )})

Imagine a stick moving with translational velocity $\vec v$ as shown below. The stick is the black line and $\vec v$ is perpendicular to the stick. The z and x components of $\vec v$ would be $v_z= v \cos \theta$ and $v_x = v \sin \theta$.

The points of intersection of the stick with the z and x axes are shown in green. The speed at which the intersection with the z-axis moves along the z-axis is $u_z = \frac{v}{\cos \theta}$. Similarly, for the speed of the intersection along the x-axis, $u_x = \frac{v}{\sin \theta}$.

$u_z$ and $u_x$ are not the z and x components of the velocity of some single point. In particular, they are not the z and x components of the velocity of some point on the stick. So, we do not expect $v = \sqrt {u_z^2+u_x^2}$.

The textbook uses the notation $v_{pz}$ and $v_{px}$ for $u_z$ and $u_x$. These should not be confused with the $z$ and $x$ components of the vector $\vec v$: $v_z$ and $v_x$.

 

[baby_1]

I see the Like is nothing to thank you. I really appreciate your explanations and the time you spent to draw the shape and explain more and more.

 

[TSny]

You are welcome.