Physics Challenge: Spherical Ball Rolling on a Rough Sphere | Just for Fun!

[etotheipi]

Just for fun!
Feel free to have a go at any of the problems.

Problem 1
A spherical ball of radius $a$ and centre $C$ rolls on the rough outer surface of a fixed sphere of radius $b$ and centre $O$. Show that the radial spin $\boldsymbol{\omega} \cdot \mathbf{c}$ is conserved where $\mathbf{c} = \mathbf{c}(t)$ is a unit vector in the direction $\overrightarrow{OC}$. Show further that$$7(a+b) \mathbf{c} \times \ddot{\mathbf{c}} + 2an \dot{\mathbf{c}} + 5g \mathbf{c} \times \mathbf{k} = \mathbf{0}$$where $n := \boldsymbol{\omega} \cdot \mathbf{c}$ and $\mathbf{k}$ is a vertical unit vector. Compare this to the equation of motion of a spinning top and deduce that the ball can roll on the surface without ever falling off!Problem 2
A relativistic particle moves in a potential $V(x) = \frac{1}{2}m \Omega^2 x^2$. The Lagrangian is $$L(x, \dot{x}) = mc^2\left[ 1- \left(1- \frac{\dot{x}^2}{c^2} \right)^{1/2} \right] - V(x)$$Show that the period of oscillations of amplitude $a$ is $\tau = \frac{2\pi}{\Omega} \left( 1 + \frac{3}{16} \epsilon^2 + \mathcal{O}(\epsilon^4) \right)$ where $\epsilon := \Omega a /c$ is small. [Hint: $h := \frac{\partial L}{\partial \dot{x}} \dot{x} - L$ is a constant of motion!]Problem 3
A light elastic string is stretched between two points $A$ and $B$ a distance $(n+1)a$ apart, and $n$ particles of mass $m$ are attached to the string at regular intervals. Each of the $n+1$ sections of string has spring constant $k$. If the system performs longitudinal oscillations along the line $\overline{AB}$ then show that the normal frequencies $\omega$ satisfy$$\Delta_n = \begin{vmatrix}
2\cos{\theta} & -1 & 0 & \dots & 0 & 0 \\
-1 & 2\cos{\theta} & -1 & \dots & 0 & 0 \\
0 & -1 & 2\cos{\theta} & \dots & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \dots & 2\cos{\theta} & -1 \\
0 & 0 & 0 & \dots & -1 & 2\cos{\theta}\end{vmatrix} = 0$$where $\cos{\theta} = 1- m\omega^2 / 2k$, and by expanding the determinant along the top row hence show that$$\Delta_n = 2\cos{\theta} \Delta_{n-1} - \Delta_{n-2}$$Solve this recursion relation for $\Delta_n$ and deduce the normal frequencies of the system.Problem 4
A vertical beam of light of power $P$ and radius $a$ is incident on the base of a glass hemisphere of radius $R$, weight $W$ and refractive index $n$. Given that $a \ll R$, determine the power $P$ of the beam such that the hemisphere hovers in static equilibrium. Neglect all terms in $(a/R)^3$ or higher order.

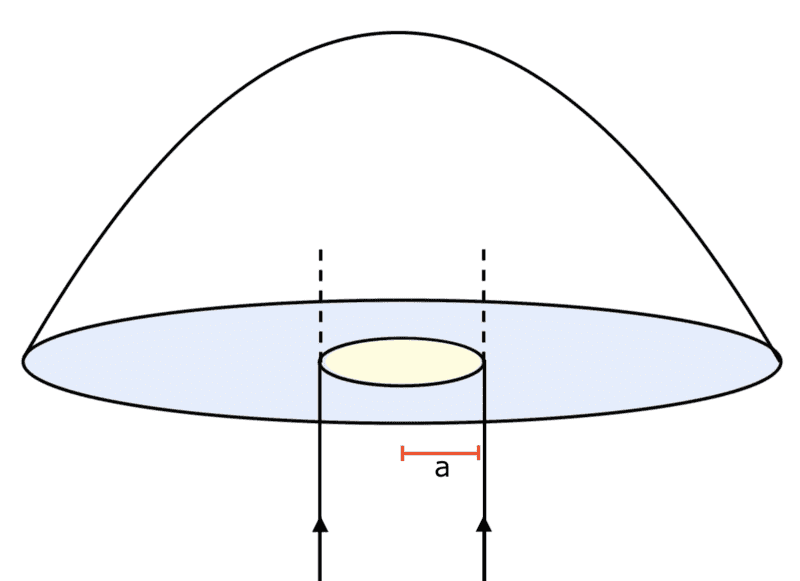
Problem 5
A particle moves in a potential $V$ with helical symmetry; $V$ is invariant under a rotation by angle $\alpha$ about the axis $Oz$ composed with a translation $c\alpha$ in the $z$ direction. What is the conserved Noether charge corresponding to this symmetry?

Problem 6 (solved by @kshitij)
Calculate the magnitude of the magnetic field produced by a square loop of side length $a$ and carrying a current $I$ at a point a distance $x$ along the axis of the loop from the centre of the loop.

 

[kshitij]

Problem 6
From symmetricity, the total magnetic field at $x$ due to the loop should 4 times the magnetic field at $x$ due to each side times the . {see figure}

magnetic field due to straight wire of finite length is,
$$B=\frac {\mu_oI[\sin\alpha+\sin\beta]} {4\pi r}$$
here, $\sin\alpha=\sin\beta=\frac a {2\sqrt{(\frac a 2)^2+r^2}}$
and $r=\sqrt{(\frac a 2)^2+x^2}$

on putting these values we should get,

Magnetic field due to loop, see edit

Edit: I forgot that we would also have to multiply the answer by $\sin\theta$ (see figure) the $\cos$ component cancels out,

So the final answer should be,
$$B= \frac {4\mu_oIa^2} {\pi (4x^2+a^2)\cdot\sqrt{(4x^2+2a^2)}}$$

Edit(II): I also used the wrong value of $\sin\alpha$ initially.

 

[etotheipi]

There's a mistake [now corrected] near the beginning of your work; note that $\sin{\alpha}=\sin{\beta} = \frac{a}{2} \cdot \frac{1}{\sqrt{r^2 + \frac{a^2}{4}}} = \frac{a}{2\sqrt{x^2 + \frac{a^2}{2}}}$ instead of $a/2r$. It should be clear why if you draw a plan view of the triangle you constructed. Try fixing that and see what you get! And as you mentioned in the edit, with your method you do also need to take into account the factor of $\sin{\theta} = a/2r$ to get the projection onto the $x$-axis.

Also, I managed to reproduce your formula for the magnitude of the field due to a finite wire but it'd be good to also show where that comes from, i.e. do the Biot-Savart integral!

 

[kshitij]

There's a mistake near the beginning of your work; note that $\sin{\alpha}=\sin{\beta} = \frac{a}{2} \cdot \frac{1}{\sqrt{r^2 + \frac{a^2}{4}}} = \frac{a}{2\sqrt{x^2 + \frac{a^2}{2}}}$ instead of $a/2r$. It should be clear why if you draw a plan view of the triangle you constructed. Try fixing that and see what you get! And as you mentioned in the edit, with your method you do also need to take into account the factor of $\sin{\theta} = a/2r$.

Also, I managed to reproduce your formula for the magnitude of the field due to a finite wire but it'd be good to also show where that comes from, i.e. do the Biot-Savart integral!

There were lots of mistakes in my answer, hopefully its now corrected

 

[etotheipi]

Looks right with the edit! Nice work

The general approach is to do the Biot-Savart integral $\mathbf{B}(1) = \frac{\mu_0}{4\pi} \int \frac{I \mathbf{e}_{12} \times d\mathbf{s}_2}{r_{12}^2}$, which in this case for a single wire turns out to have an $x$-component\begin{align*}

B_x &= \frac{-\mu_0 I}{4\pi} \int_{-a/2}^{a/2} \frac{a/2}{(x^2 + \frac{a^2}{4} + t^2)^{3/2}} dt \\

&= \frac{-\mu_0 I}{4\pi} \cdot \frac{a^2}{2(x^2 + \frac{a^2}{4})\sqrt{x^2 + \frac{a^2}{2}}} \\

&= \frac{-\mu_0 I a^2}{\pi(4x^2 + a^2)\sqrt{4x^2 + 2a^2}}

\end{align*}which you then multiply by $4$, using the symmetry, to get the final result.

 

[Keith_McClary]

I noticed these questions aren't getting so much traction.

Aren't you aiming for a month's worth of effort?

 

[etotheipi]

Here are my solutions, just check yours against them. Sorry if there are any typos or mistakes.

Spoiler: Problem 1

Let the weight be $-mg \mathbf{k}$ and the contact force from the sphere be $\boldsymbol{\xi}$. Take moments about the centre of mass:$$\mathbf{G} = (-a\mathbf{c}) \times \boldsymbol{\xi} = I \dot{\boldsymbol{\omega}}$$Newton's second law:$$m\dot{\mathbf{v}} = -mg\mathbf{k} + \boldsymbol{\xi}$$the rolling condition:$$\mathbf{v} + \boldsymbol{\omega} \times (-a \mathbf{c}) = \mathbf{0}$$and finally the relation $\mathbf{r} = (a+b)\mathbf{c}$ and its time derivatives. We will eliminate $\boldsymbol{\xi}$ to write$$mga \mathbf{k} \times \mathbf{c} + ma(a+b) \ddot{\mathbf{c}} = I \dot{\boldsymbol{\omega}}$$but for a sphere $I = \frac{2}{5}ma^2$ thus$$g\mathbf{k} \times \mathbf{c} + (a+b) \ddot{\mathbf{c}} = \frac{2}{5} a \dot{\boldsymbol{\omega}} \quad \quad \quad (1)$$Next, notice that $(a+b) \dot{\mathbf{c}} \cdot \boldsymbol{\omega} = (a\boldsymbol{\omega} \times \mathbf{c}) \cdot \boldsymbol{\omega} = 0 \implies \dot{\mathbf{c}} \cdot \boldsymbol{\omega} = 0$ and also that from the moment equation $0 = \mathbf{c} \cdot (-a\mathbf{c}) \times \boldsymbol{\xi} = I \mathbf{c} \cdot \dot{\boldsymbol{\omega}} \implies \dot{\boldsymbol{\omega}} \cdot \mathbf{c} = 0$. It immediately follows that $\frac{d}{dt}(\boldsymbol{\omega} \cdot \mathbf{c}) = 0$. Thus $\boldsymbol{\omega} \cdot \mathbf{c} := n$ is a conserved quantity. Let's now differentiate the rolling condition and then take the cross product on the left with $\mathbf{c}$,\begin{align*}
\dot{\mathbf{v}} &= a\dot{\boldsymbol{\omega}} \times \mathbf{c} + a\boldsymbol{\omega} \times \dot{\mathbf{c}} \\

(a+b) \mathbf{c} \times \ddot{\mathbf{c}} &= a(\mathbf{c} \cdot \mathbf{c}) \dot{\boldsymbol{\omega}} - a(\mathbf{c} \cdot \dot{\boldsymbol{\omega}})\mathbf{c} + a (\mathbf{c} \cdot \dot{\mathbf{c}})\boldsymbol{\omega} - a (\mathbf{c} \cdot \boldsymbol{\omega}) \dot{\mathbf{c}}

\end{align*}but $\mathbf{c} \cdot \mathbf{c} = 1$, and $\mathbf{c} \cdot \dot{\mathbf{c}} = 0$ and also with $n := \boldsymbol{\omega} \cdot \mathbf{c}$ then$$a \dot{\boldsymbol{\omega}} = an\mathbf{c} + (a+b) \mathbf{c} \times \ddot{\mathbf{c}}$$Finally we may substitute this into equation $(1)$ to obtain, $$0 = 2an \mathbf{c} + 7(a+b) \mathbf{c} \times \ddot{\mathbf{c}} - 5g\mathbf{k} \times \mathbf{c}$$which is the desired result up to a re-arrangement.

Spoiler: Problem 2

$T$ and $V$ for the system are\begin{align*}
T &= \frac{1}{2} m\sum_i^N \dot{x}_i^2 \\
V &= \frac{1}{2} k \sum_i^{N-1} (x_{i+1} - x_i)^2
\end{align*}Expressing $V = \sum_j \sum_k v_{jk} x_j x_k$ and $T = \sum_j \sum_k t_{jk} \dot{x}_j \dot{x}_k$ we collect the coefficients into matrices $V = (v_{jk})$ and $T = (t_{jk})$. In this case it's clear that\begin{align*}

T = \frac{1}{2} m \, \mathrm{diag}(1, \dots, 1)

\end{align*}and for $V$\begin{align*}
V = \frac{1}{2} k
\begin{pmatrix}
2 & - 1 & 0 & \dots & 0 & 0 \\
-1 & 2 & -1 & \dots & 0 & 0 \\
0 & - 1 & 2 & \dots & 0 & 0 \\
\vdots & \vdots & \vdots \\
0 & 0 & 0 & -1 & 2 & - 1 \\
0 & 0 & 0 & 0 & -1 & 2
\end{pmatrix}\end{align*}To determine the normal frequencies we look for solutions of $\mathrm{det}(V - \omega^2 T) = 0$ or equivalently $\mathrm{det}(2V - 2\omega^2 T) = 0$ which when written out gives the required result. Expanding the determinant of $\Delta_n$ across the top row yields the recurrence relation which we will solve by guessing $\Delta_q = \sin(q+1) \theta / \sin{\theta}$. It's straightforward to check that this holds for $q=3$ and $q=4$ so now we assume it holds for some $q -1$ and $q-2$ and then\begin{align*}

\Delta_q &= 2\cos{\theta} \left[ \frac{\sin q\theta}{\sin \theta} \right] - \frac{\sin(q-1)\theta}{\sin{\theta}} \\

&= \frac{1}{\sin \theta} \left[ 2\cos{\theta}\sin q\theta - \sin q \theta \cos \theta + \cos q \theta \sin \theta \right] \\

&= \frac{1}{\sin \theta} \left[ \cos{\theta}\sin q\theta + \cos q \theta \sin \theta \right] \\

&= \frac{\sin(q+1)\theta}{\sin{\theta}}

\end{align*}completing the induction. Hence $\Delta_q = 0$ implies that $\sin(q+1)\theta = 0 \implies \theta = \frac{j \pi}{n+1}$. With $\cos{\theta} = 1-m\omega^2 /2k \implies \omega^2 = 2k(1-\cos{\theta})/m$ we write $2\sin^2{\frac{\theta}{2}} = 1- \cos{\theta}$ so that $\omega^2 = (4k\sin^2{\frac{\theta}{2}})/m$ and$$\omega_j = 2 \sqrt{\frac{k}{m}} \sin{\left( \frac{j\pi}{2(n+1)}\right)}$$
for $j \in [1,n] \cap \mathbb{N}$

Spoiler: Problem 3

Use that $h := \frac{\partial L}{\partial \dot{x}} \dot{x} - L$ is a constant of the motion. For this Lagrangian it is$$h = mc^2 \left(1-\frac{\dot{x}^2}{c^2} \right)^{-1/2} -mc^2 + \frac{1}{2}m \Omega^2 x^2$$the amplitude is $a$ and so $x |_{\dot{x} = 0} = a$. Define $h' = h + mc^2$, which is also a constant of motion. Thus equating $h'$ when between the point of maximum amplitude and a general point $x$ we have $mc^2 + \frac{1}{2}m \Omega^2 a^2 = \frac{mc^2}{\sqrt{1-\frac{\dot{x}^2}{c^2}}} + \frac{1}{2} m \Omega^2 x^2$. We now invert this equation for $\dot{x}$\begin{align*}

\frac{\dot{x}}{c} &=\sqrt{\frac{(mc^2 + \frac{1}{2}m \Omega^2(a^2 - x^2))^2 - (mc^2)^2}{(mc^2 + \frac{1}{2}m\Omega^2(a^2-x^2))^2}} \\ \\

\frac{\dot{x}}{c} &= \frac{\sqrt{m^2c^2\Omega^2(a^2-x^2) + \frac{1}{4}m^2 \Omega^4 (a^2-x^2)^2}}{mc^2 + \frac{1}{2} m \Omega^2 (a^2 - x^2)}

\end{align*}By separation of variables\begin{align*}

\int_0^a \frac{mc^2 + \frac{1}{4} m \Omega^2(a^2 - x^2)}{\sqrt{m^2 c^2 \Omega^2(a^2-x^2) + \frac{1}{4}m^2 \Omega^4 (a^2-x^2)^2}} dx = c \int_0^{\tau/4} dt \quad \quad \quad (1)

\end{align*}We may simplify this by noticing that $$\sqrt{m^2 c^2 \Omega^2(a^2-x^2) + \frac{1}{4}m^2 \Omega^4 (a^2-x^2)^2} = mc\Omega \sqrt{a^2 - x^2} \sqrt{1 + \frac{1}{4} \epsilon^2 \left(1- \frac{x^2}{a^2} \right)}$$and also$$mc^2 + \frac{1}{2} m \Omega^2 (a^2 - x^2) = mc^2 \left(1 + \frac{1}{2} \epsilon^2 \left(1- \frac{x^2}{a^2} \right) \right)$$Also apply the substitution $\cos^2{\theta} = 1- \frac{x^2}{a^2}$ giving $a \sqrt{1-\frac{x^2}{a^2}} d\theta = dx$. The integral is transformed into$$\frac{4}{\Omega} \int_0^{\pi/2} \frac{1 + \frac{1}{2} \epsilon^2 \cos^2 \theta }{\sqrt{1 + \frac{1}{4} \epsilon^2 \cos^2 \theta}} d\theta = \tau$$We are given that $\epsilon$ is small. Taking the binomial expansion of the denominator gives\begin{align*}

\tau &\sim \frac{4}{\Omega} \int_0^{\pi/2}(1 + \frac{1}{2} \epsilon^2 \cos{\theta})(1 - \frac{1}{8} \epsilon^2 \cos^2{\theta}) \\

&\sim \frac{4}{\Omega} \int_0^{\pi/2} 1 + \frac{3}{8} \epsilon^2 \cos^2{\theta} d\theta \\

&\sim \frac{2\pi}{\Omega} \left( 1 + \frac{3}{16} \epsilon^2\right)

\end{align*}

Spoiler: Problem 4

If the total incident power is $P$, then the incident power on a ring of radius $\delta r$ at $0 < r < a$ is$$\delta P = \frac{2\pi r \delta r}{\pi a^2} P = \frac{2P r \delta r}{a^2}$$Let this ring of light meet the top surface of the hemisphere at angle $\theta$ to the vertical. The momentum of the light entering the hemisphere per second is thus $K = (2R^2 P \sin{\theta} \cos{\theta} \delta \theta)/ca^2$ since $r = R\sin{\theta}$ and $\delta r = R\cos{\theta} \delta \theta$. Upon exiting the hemisphere, let the angle of refraction of this light to the normal of the surface be $\alpha$. The change in vertical momentum of this light per unit time is$$\delta K = K(1- \cos{(\alpha - \theta)}) \sim \frac{K(\alpha^2 - 2\alpha \theta + \theta^2)}{2}$$By Snell's law we have $n\sin{\theta} = \sin{\alpha} \implies n\theta \sim \alpha$ thus $\alpha^2 - 2\alpha \theta + \theta^2 \sim \theta^2(n-1)^2$ and$$\delta K \sim \frac{2R^2P(n-1)^2}{2ca^2} \theta^3 \delta \theta$$Now we integrate up over all rings between $0 < r < a$ to find the total force exerted by the light$$F \sim \frac{R^2 P(n-1)^4}{4ca^2} \theta_c^4$$where $\theta_c \sim a/R$ and thus$$F \sim \frac{Pa^2(n-1)^2}{4cR^2} \overset{!} = W$$which gives the required power $P \sim 4cR^2 W / a^2(n-1)^2$

Spoiler: Problem 5

Straightforward, in cylindrical coordinates write $L = \frac{1}{2}m\dot{r}^2 + \frac{1}{2}mr^2 \dot{\theta}^2 + \frac{1}{2}m\dot{z}^2 - V$. The question gives us the one-parameter family of symmetry transformations parameterised by $\alpha$, namely $(r, \theta,z) \mapsto (r', \theta', z') = (r, \theta + \alpha, z + c\alpha)$ and as usual we just need to write\begin{align*}

\mathcal{Q} &= \frac{\partial L}{\partial \dot{x}_i} \left( \frac{\partial x_i'}{\partial \alpha} \right)_{\alpha = 0} \\

&= mr^2 \dot{\theta} + mc \dot{z}

\end{align*}

 

[hutchphd]

For P:roblem #4 the Force limit for large n (very very slow glass) should not go to infinity..somehow there should be an $n^2$ in the denominator. You cannot assume $\theta$ small if n gets large even if it is small compared to R.

 

[etotheipi]

For P:roblem #4 the Force limit for large n (very very slow glass) should not go to infinity..somehow there should be an $n^2$ in the denominator. You cannot assume $\theta$ small if n gets large even if it is small compared to R.

the force does diverge, but the power does not diverge, if $n \rightarrow \infty$
(we assume no light is reflected internally, so $\theta$ may still be assumed small in limit of large $n$)

i.e. the $(n-1)^2$ is on the denominator
$P \sim 4cR^2 W / a^2(n-1)^2$

 

[hutchphd]

Why would the Force diverge? I think the physics of n large would just be the same as absorbing the whole beam because of total internal reflection if nothing else...How would you get infinite force? So your approximation is more a than limit on a/R.

I think a more careful treatment of the surface shape will get you there. Can't do it right now...

 

[etotheipi]

there is no mistake

because of total internal reflection if nothing else.

internal reflections are neglected

I think a more careful treatment of the surface shape

it is a hemisphere!

 

[Office_Shredder]

To settle this, you obviously need to get a glass hemisphere and a laser and see if you can make it float at the predicted power. YouTube video or it didn't happen

 

[hutchphd]

Charge up the flux capacitor!

 

[hutchphd]

OK I worked it through and you are exactly correct, although the expansion parameter is in fact (n-1) a/R so my limiting case is excluded.
I guess I'll put the flux capacitor back in the box. I wasn't sure where I'd get the 1.21 gigawatts anyhow.

 

[hutchphd]

if n→∞
(we assume no light is reflected internally, so θ may still be assumed small in limit of large n)

I note also that 1.21 gigawatts is just about the power level required if this lens is a macroscopic object!

 

[Keith_McClary]

Ah, you want it to be hard! Okay, I like your style. I deleted the hints.

How many answers (besides yours) do the Math Challenge questions get in a week?

 

[fresh_42]

How many answers (besides yours) do the Math Challenge questions get in a week?

The math challenge threads are a black body ...