pilot12
- 5
- 0
- Homework Statement
- Trouble on this final problem of my physics homework
- Relevant Equations
- M g h + 1/2 mv^2 - (s1+s2)umg=0
h= 1.18sin(28.1) = .55579
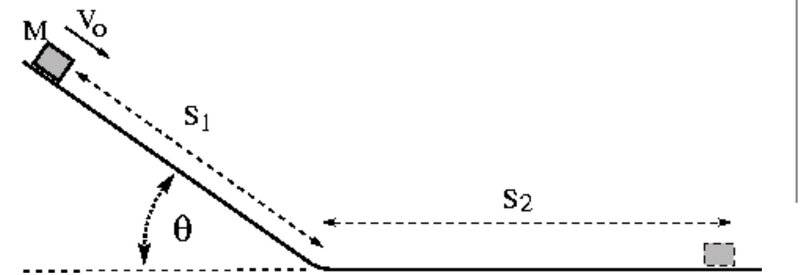
When mass M is at the position shown, it is sliding down the inclined part of a slide at a speed of 2.19 m/s. The mass stops a distance S2 = 2.1 m along the level part of the slide. The distance S1 = 1.18 m and the angle θ = 28.10°. Calculate the coefficient of kinetic friction for the mass on the surface.
https://letu.loncapa.net/res/msu/physicslib/msuphysicslib/13_EnergyConservation/graphics/prob27a_MechEnWFriction.gif
https://letu.loncapa.net/res/msu/physicslib/msuphysicslib/13_EnergyConservation/graphics/prob27a_MechEnWFriction.gif
Last edited:
 ##\qquad##!
##\qquad##!