Planck's law (wavelength, frequency, angle?)

[Lamdbaenergy]

So I was just looking around today and stumbled upon something called Planck's law. I saw an equation and quite few more of them that looked like this,

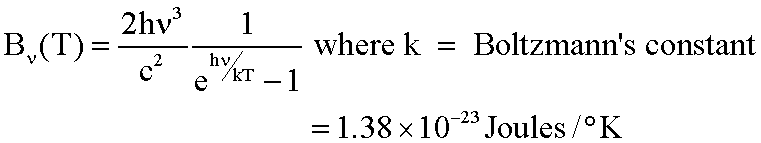
I'm familiar with all of the other variables and constants already, but don't get the E (hv/kT) part, yet. Is E the energy of the photons you are supposed to raise it to by the POWER of (hv/kT)? And what does the result you get from this whole equation tell you about the radiation coming out of the black body? Don't blind me with too much math if you don't really have to and thanks!

 

[ChrisVer]

that e is the exponential of (hv/kT), not the energy. You can also see it written as $\exp ( \frac{hv}{kT} )$. The exponential is the solution to the problem:
$$ \ln x = a \Rightarrow x = e^a$$
... the energy of the photon is the $E=hv$...
What does it tell you? it tells you that the black body radiation has a certain distribution in energies/frequencies. In general it radiates in all the frequency spectrum, however there is a certain peak-value at its distribution, characterizing the black body... If you look it around you will find how the distribution looks like...

However you can see that for large $E \rightarrow \infty$ this will fall exponentially since:
$$ B \propto \frac{Ε^3}{e^{E/kT} -1 } \approx \frac{Ε^3}{e^{E/kT}} = Ε^3 e^{- E/kT} \rightarrow 0$$

also for small energies $E \rightarrow 0$ this allso falls to zero, because of the energy on the nominator... $h v^3 = \frac{E^3}{h^2}$ whereas the exponential can be Taylor expanded to $e^{E/kT} \approx 1+ \frac{E}{kT}$ so the $B$ goes as $E^2$ for small energies, thus goes to zero.
It will have a maximum at some energy $E_\gamma$ where $\frac{dB}{dE}=0$...

Also it gives you information about the temperature. Different temperature black-bodies will show a different distribution...