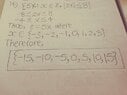- #1
Please check/confirm if the set is correct
- Thread starter Math100
- Start date
-
- Tags
- Set
In summary, the conversation is about someone asking for confirmation of a set and then making corrections based on a reminder. The final set is simplified and presented in a more precise and professional manner. It is also noted that the statement following "therefore" should be a statement, not just an expression.
- #2
- 19,712
- 25,689
Almost. What about ##x=\pm 4##?Math100 said:
- #3
Math100
- 797
- 221
Oh, yes! You just reminded me something. I am so sorry, I forgot that this is a closed interval where both 4 and -4 are included in the set.fresh_42 said:
- #4
- #5
- 19,712
- 25,689
That's ok. You could write it in the following way if you want to be precise:Math100 said:
\begin{align*}
\{5x\,|\,x\in \mathbb{Z}\wedge |2x|\leq 8\}&=5\cdot \{x\in \mathbb{Z}\,|\,2\cdot |x|\leq 8\}=5\cdot \{x\in \mathbb{Z}\,|\, |x|\leq 4\}\\&=5\cdot \{x\in \mathbb{Z}\,|\, -4\leq x\leq 4\}=5\cdot\{-4,-3,-2,-1,0,1,2,3,4\}\\
&=\{-20,-15,-10,-5,0,5,10,15,20\}
\end{align*}
(edited to make it shorter)
- #6
Math100
- 797
- 221
Thank you so much for this! I think this is much more precise and professional! I've never seen this before!fresh_42 said:
- #7
Mark44
Mentor
- 37,781
- 10,170
As a minor point, whatever follows "therefore" should be a statement, such as an equality or inequality, not just an expression, such as {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Following @fresh_42's work, you could conclude something like this:
Therefore, ##\{5x\,|\,x\in \mathbb{Z}\wedge |2x|\leq 8\} =\{-20,-15,-10,-5,0,5,10,15,20\}##
Following @fresh_42's work, you could conclude something like this:
Therefore, ##\{5x\,|\,x\in \mathbb{Z}\wedge |2x|\leq 8\} =\{-20,-15,-10,-5,0,5,10,15,20\}##
- #8
Math100
- 797
- 221
Thank you for pointing that out, I will keep that in mind.Mark44 said:
FAQ: Please check/confirm if the set is correct
What does it mean to "check/confirm if the set is correct"?
When someone asks you to check or confirm if a set is correct, they are asking you to review the elements in the set and determine if they are accurate, complete, and in the correct order.
How do you check if a set is correct?
To check if a set is correct, you can compare it to a known correct set or use a specific set of criteria to evaluate the elements. This may involve checking for errors, verifying the order of elements, or confirming the completeness of the set.
Why is it important to check if a set is correct?
Checking if a set is correct is important because it ensures accuracy and consistency in data or information. It also helps to identify and correct any errors or discrepancies in the set, which can impact the overall validity and reliability of the data.
What happens if a set is incorrect?
If a set is incorrect, it means that there are errors, missing elements, or elements in the wrong order. This can lead to inaccurate data and potentially impact the results or conclusions drawn from the data. It is important to correct any errors and ensure the set is accurate before using it for analysis or decision making.
Are there any tools or techniques that can be used to check if a set is correct?
Yes, there are various tools and techniques that can be used to check if a set is correct. These may include data validation software, manual review and comparison, or statistical analysis. The specific tool or technique used will depend on the type of data and the purpose of the set.