Please help me find what 't' is (Plane flying across the Atlantic Ocean)

[Thickmax]

Homework Statement

I can work out a formula, but I am missing a value, so cannot solve it.

Please can my formula be checked?

Relevant Equations

See below

Please see below question and formula for Z(t) - position,

I differentiate twice to get the below formula for acceleration.

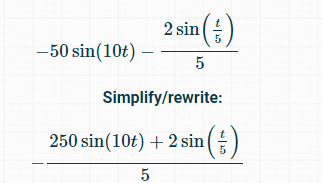
But I cannot solve it because of the unknown t...

What is t representing in the original equation?

 

[Frabjous]

Think about why you took the second derivative.

 

[Thickmax]

to get the acceleration?

 

[Frabjous]

Yes. If taking the second derivative with respect to t gives you the acceleration,
t must be …

 

[Thickmax]

time?

 

[Frabjous]

Yes. So you now have derived a function for acceleration. Do you now how to find a maximum or minimum of a function using calculus?

 

[Thickmax]

Maybe...I don't really know what it entails without an example...

Maximum value of a sine wave is 1, so is it just 1 as we are looking at the maximum?

 

[Frabjous]

Is there a value of t where both of the sine functions = -1 (negative because of the negative sign in front of the sine)

 

[Thickmax]

I'm sorry, I really don't know...I cannot think of a number where you multiply it by 10 and 5th it to get sin(-1)...

 

[Frabjous]

Let t=5s
You then end up with sin(50s) and sin(s), so when s is a multiple of π/2, 50s is a multiple of 25π so they do not reach maximums at the same time.

Think back to calculus. Functions are at a maximum or minimum when you set their derivative equal to zero.

 

[Frabjous]

Are you allowed to do things numerically? I am not seeing a simple analytical solution.

 

[Thickmax]

You're going to have to realize I'm the biggest idiot on this forum and saying these things is going to be painful!

I think I need to do them numerically, but I don't even know if I'm meant to be working in radians or degrees...

I agree with your principle of t=5s, but I'm don't see how I can use t=5s in the question...

 

[Frabjous]

Sine functions equal +-1 when they are odd multiples of pi/2
They equal 0 when they are multiples of pi
knowing this, the t=5s substitution shows that the two sine functions are not maximums at the same time

 

[Frabjous]

Since you are allowed to do this numerically, just find the maximum of the equation you derived originally. Sorry i could not be of more help.

 

[Frabjous]

Actually, there is a trick. They want only 2 significant digits. If you look at your equation, we know that the maximum is bounded.
50-0.4≤maximum≤50+0.4
49.6≤maximum≤50.4
since we only want 2 digits
50≤maximum≤50
therefore the answer is 50m/s²

 

[haruspex]

Because of the great difference in the amplitudes, you know the max will be near $10t=2n\pi-\pi/2$ for some integer n.
Because the expression as a whole is periodic, you can assume 0<n<50.
What does that give for t/5? What value of n will also make sin(t/5) close to -1?
Having chosen n, you can set $10t=2n\pi-\pi/2+\epsilon$ and use the expansion of cos(x) for small x to get a quadratic for $\epsilon$.

Edit: For some reason, there is often a long delay before others' posts become visible to me. I posted post #16 before post #15 showed up. Anyway, you can use post #16 to get a more accurate solution.

 

[Delta2]

Wolfram says that the maximum is the one where both terms are maximized, that is equal to 50+2/5. You can test this by trying to solve the system $$\sin10 t=1$$$$\sin0.2t=1$$ and see if they have common t-values.

EDIT: What I am saying here is not 100% accurate but it might be approximately correct. Please check the two posts below.

 

[haruspex]

Wolfram says that the maximum is the one where both terms are maximized, that is equal to 50+2/5. You can test this by trying to solve the system $$\sin10 t=1$$$$\sin0.2t=1$$ and see if they have common t-values.

As @caz noted in post #13, there is no such solution. 0.2t would have to be an odd multiple of pi/2. That would make 10t an even multiple of pi/2.

 

[Delta2]

As @caz noted in post #13, there is no such solution. 0.2t would have to be an odd multiple of pi/2. That would make 10t an even multiple of pi/2.

You might be right, a more careful reading of the wolfram output, says that the maximum is 1.99951 and not 2 (looked for maximum of sin10t+sin0.2t)

Check this
https://www.wolframalpha.com/input/?i=plot+y=sin(10t)+sin(0.2t),y=2+from+t=5+to+t=10

it seems that $\sin 10 t+\sin 0.2 t$ gets very close to 2 for some t between 5 and 10.

 

[Thickmax]

Actually, there is a trick. They want only 2 significant digits. If you look at your equation, we know that the maximum is bounded.
50-0.4≤maximum≤50+0.4
49.6≤maximum≤50.4
since we only want 2 digits
50≤maximum≤50
therefore the answer is 50m/s²

You are right with the answer of 50, but can you please explain where are you getting 0.4 from?

 

[Delta2]

You are right with the answer of 50, but can you please explain where are you getting 0.4 from?

I think its from the coefficient $\frac{2}{5}$ of the term $\frac{2}{5}\sin \frac{t}{5}$. This term has minimum $-\frac{2}{5}$ and maximum $\frac{2}{5}$.

 

[Frabjous]

You have two sine functions. One has an amplitude of 50 and the other 0.4
If the 2 functions reach their maximum values at the same time, their amplitudes add.
If the 2 functions reach a maximum and a minimum at the same time, their amplitudes subtract.
These 2 conditions are bounds for the maximum value of their sum.

Note: I am being sloppy in regards to signs (not sines)

 

[Thickmax]

right, so because the maximum value sin(t/5) can be is 1, and then -1,

So if t in this equation is 450, the value of sin(90) is maximum, then 2/5 of 1=0.4

and then for the same reason in the first part, sin(90) is maximum = 1. Then 50 times this or -50 times this...

the value of t doesn't matter as we are looking at the maximum, which will always be 1.I'm not sure I'd be ever able to see these jumps without plugging and chugging, or having a question explained to me.

Thank you very much for your help.

 

[Frabjous]

Notice that ω is defined in rad/s, so you are making some unit mistakes.

 

[Frabjous]

I'm not sure I'd be ever able to see these jumps without plugging and chugging, or having a question explained to me.

My generic advice is pay attention to the physics. It is too easy to get wrapped up in mathematical manipulation and to forget that you are trying to calculate something physical.

That being said, I learned to do physics before tools like wolframalpha were available. If I was learning it today, I would probably have jumped to numerics at some point.

 

[Thickmax]

My generic advice is pay attention to the physics. It is too easy to get wrapped up in mathematical manipulation and to forget that you are trying to calculate something physical.

That being said, I learned to do physics before tools like wolframalpha were available. If I was learning it today, I would probably have jumped to numerics at some point.

Thanks Caz, I'll keep this in my mind the next time I attempt this course!